Diese Seite ist auch in deutsch erhältlich.
-> Back to Index without frames - Activate frames and permanent directory
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
An aliquot sequence is a sequence of integers, built with
the sigma function. sigma(n) or s(n) is the sum of divisors of an integer
n.
The sum
of
the proper divisors is
i(n) = sigma(n) - n
Iterate: i(n) = sigma(n) - n, i(i(n)) = sigma(i(n)) - i(n) and so on. 276:i4
means the fourth iteration in the sequence starting with 276. This sequence
begins with 276, 396, 696, 1104, 1872 - 276:i4 is 1872. You can look at the complete sequence
with this link: 276
or at the graph.
Normally an aliquot sequence ends in a prime. Different sequences
can come together and end in the same prime. All these side sequences are called a prime family
(Primzahlfamilie). New calculations occasionally lead to a
confluence of two former different aliquot sequences into one family.
This was first published by the Belgian mathematician Eugène Catalan in the
year 1888.
Leonard Eugene Dickson extended the so called Catalan
conjecture: "Each aliquot sequence ends in a prime,
in a perfect number or in an aliquot cycle".
Up to now it is not possible to certify the Catalan conjecture.
Each confluence of two sequences gives some more hope, but it's no proof of the conjecture, it's only some work on the way to possible solution. A great step in this direction was done in February 2005 from Christophe Clavier. He found the confluence of sequence 1578 and 56440 with a record descent from C110 down to C5
The term "Catalan's Conjecture" is used for another
mathematical problem, too:
Catalan's conjecture states that the equation xm
- yn = 1 has no other integer solution but 32
- 23 = 1. In May 2002 Preda
Mihailescu gave a proof for this conjecture. On this website you can't find
anything else about these facts.
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
An ending aliquot sequence is a so called terminating sequence.
Normally the end of an aliquot sequence is a prime.
Instead of a prime an aliquot sequence can end in a cycle,
too. Well known are amicable pairs. Pythagoras said true
friendship is comparable to the numbers 220 and 284 - this is the
smallest amicable pair: i(220) = 284 and i(284) = 220. Meanwhile
thousands of amicable pairs are found. Most of them are constructed with the
help of
Thabit rules.
Pedersen counted more than
11994387 (on October, 1st, 2007) amicable pairs mostly in the interval [1,
10^999],
some of them in [10^1000, 10^13581]. Up to 10^14 the listing is exhaustive. You will find
links to all pair and notes to the explores.
Note: Pedersen's data get updated in short intervals.
Some cycles are of higher order (so called sociable numbers). Cycles with 4, 5,
6, 8, 9 and 28 members are known. Other orders are possible, too. Today (February
2015) we know 237 aliquot cycles
with higher order.
David Moews
shows a complete listing of all known aliquot cycles, Jan
Pedersen
shows a comparable table, too. The sequence with the key-number 17490
ends in an aliquot-4-cycle. There are 226 cycles of the order 4, five of the order
6, three of the order 8, one of the order 5, 9 and 28. Up to 5*10^12 the listing for
aliquot-4-cycles is exhaustive. The largest 4-cycle has 71 digits.
The smallest cycles are the perfect numbers. Their sum of
divisors is doubled n and i(n) = n. The smallest perfect numbers
are 6, 28, 496, 8128, 33550336. Today there are 48 perfect
numbers known (Mersenne prime no. 42 was found in February 2005,
no. 43 in December 2005, no. 44 in September 2006, no.45
in August 2008, no. 46 in September 2008, no. 47 in June 2009, no.
48 in January 2013). Their greater prime factor is a Mersenne
prime. To my knowledge it is not yet known whether all perfect numbers are
even or not. Brent, Cohen and te Riele gave a lower bound of 10^300 for odd
perfect numbers.
There is a search of such numbers (GIMPS) in the world wide web. The Mersenne prime no. 43 has 9152052
digits, no. 44 has 9808358
digits, no. 45 has 12978189 digits. The others are a little bit smaller (for
details have a look on GIMP, please). The record is no. 48 with 17425170 digits.
Several sequences are not computed up to their end. They are increasing and no one knows if they will end or not. The smallest
start-up
number (or key-number, beginning number) of such a so-called open-end sequence (OE-sequence -
Offenendkette) is 276 (-> labyrinth
of
Chartres). An open-end sequence with all side sequences
is called an open-end family (OE-family).
There are 5 open-end sequences in the interval [1, 1000] with the key numbers
276, 552,
564, 660 und
966. They are called
Lehmer Five.
There are 81 open-end-sequences in the interval [1, 10^4].
There are now 898 open-end sequences in [1, 10^5] and 9190 OE-sequences in [1, 10^6].
Any progress in calculation can reduce these numbers.
The following table shows the actual limits of
computation (B = Bosma, C = Creyaufmueller, CL = Clavier, G = Gerved, H=Hoogendoorn, S = Stern, VB =
Varona/Benito, Z = Zimmermann) and the
number of open-end sequences. A detailed
table
shows more intervals. Varona gives an overview at [1,10^4].
New are the tables for [1,
220000].
Table - overview :
|
interval |
number of OE- sequences |
limits of computation |
computed by |
| [1, 1000] | 5 | > 10^186 | C/Z |
| [1, 10000] | 81 | > 10^151 | C/VB/Z/CL |
| [1, 50000] | 440 | > 10^100 | B/C/G/VB |
| (50000, 10^5] |
458 |
> 10^100 | C/G/S/Z |
| [1, 100000] | 898 | > 10^100 | B/Z/G/VB/S/C/CL |
| (100000, 200000] | 950 | > 10^100 | C/VB |
| (200000, 300000] | 911 | > 10^80 / 10^100 | C / H / B |
| (300000, 400000] | 850 | > 10^80 / 10^100 | C/B |
| (400000, 500000] | 882 | > 10^80 | C |
| (500000, 600000] | 945 | > 10^80 | C |
| (600000, 700000] | 932 | > 10^80 | C |
| (700000, 800000] | 919 | > 10^80 / 10^100 | C |
| (800000, 900000] |
952 |
> 10^80 | C |
| (900000, 10^6] | 951 | > 10^80 | C |
| [1, 10^6] | 9190 | > 10^80 / 10^100 | |
| Download all OE-Sequences | > 10^80 / 10^100 | ||
A group of free workers will do lots of work on aliquot sequences. To avoid multiple work please check the website of Mersenne-Forum for reserved sequences! (200k, 250k] is up to >C100. (500k, 600k] is reserved.
About 1% of all integers are beginning numbers (key numbers) of an open-end
sequence. This is an empirical result. Have a look at the complete
statistic in [1, 10^6], click here
for download.
Attention: Please have a look on Richard K. Guy's 'Law
of Small Numbers'.
The table above is the result of long calculations. The program
Aliquot
by Ivo Duentsch produces a record file (so-called matrix). Each integer
is related to its target. Each aliquot sequence was computed up to its end or up
to a break, if the sequence grows too much. These open-end sequences were
computed separately with UBASIC-programs.
The data for the interval [1, 10^6] have increased up to
several Gigabytes during several years.
All sequences were checked for combinations. Side sequences got the newly found
prime. Side sequences of OE-sequences got the smallest key-number comparable to
a target-prime.
Each sequence in the whole interval up to 10^6 was checked up to 40 digits in a
first step. In a second step this upper limit was expanded to a minimum of 60
digits. These complex calculations were finished in May 1999. The third step is
the expanded calculation up to 80 digits. These calculations were finished end
of March 2003.
In the meantime a few more sequences have been terminated. The table above
includes all known terminating sequences in the statistic.
The extension of calculation limit from C60 up to C80 reduces the number of OE-sequences about 2 - 2.5%. Some sequences terminate, the other were identified
as side-sequences.
At Christmas 2001 Varona terminated the sequence 6160 and 1797 numbers in (1,
10^6] changed their family status.
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
To get a general idea a graphic presentation of an aliquot
sequence is helpful using a semi logarithm axis, i.e. a linear x-axis beginning
with 0 for the index number of the sequence and the y-axis on a scale of decadic
logarithm for the sum of the proper divisors.
So there is a function f: N(n) -> log10 i(n).
There are three types of aliquot sequences and three types of diagrams, too.
| 1) terminating sequences | The graph is a single irregular peak (ending in a prime number) | Example: g840 |
| 2) cyclic ending | The graph ends in a horizontal line (ending in a perfect number) | Example: g976950 |
| The graph alternates between two horizontal asymptotic lines (ending in a pair of amicable numbers) | Example: g980460 | |
| The graph alternates between two horizontal asymptotic lines (ending in an aliquot cycle) | Example: g17490 und g2856 | |
| 3) open-end sequence | The graph ascends and has it's maximum often at the last calculated term | Example: g276 |
Additional diagrams will be seen with the help of the links on the record list or on the additional page "Lehmer Five".
up 840 976950 980460 17490 2856 276 1578 down
840 - terminating sequence (complete sequence)

up 840 976950 980460 17490 2856 276 1578 down
976950 - ending in perfect number (6)
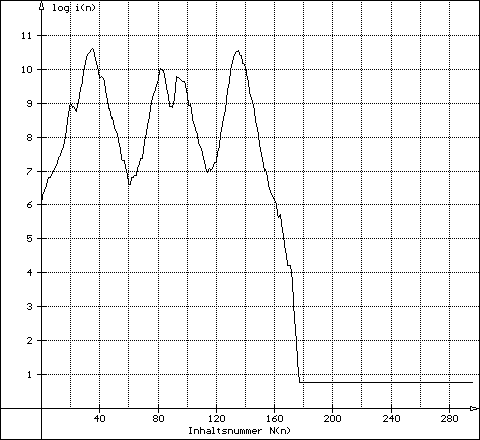
up 840 976950 980460 17490 2856 276 1578 down
980460 - ending in an amicable pair (2620/2924)
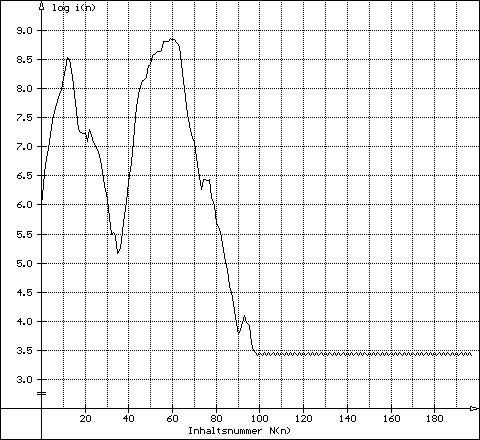
up 840 976950 980460 17490 2856 276 1578 down
17490 - ending in an aliquot 4-cycle
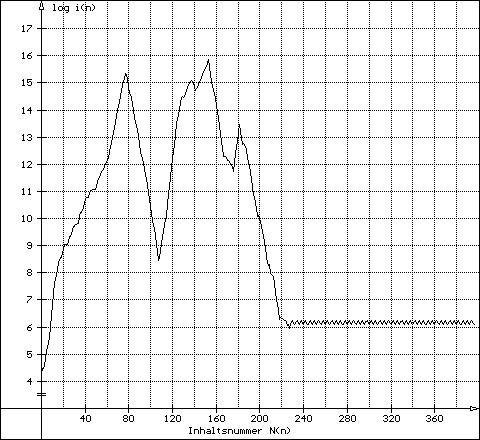
up 840 976950 980460 17490 2856 276 1578 down
2856 - ending in the aliquot 28-cycle
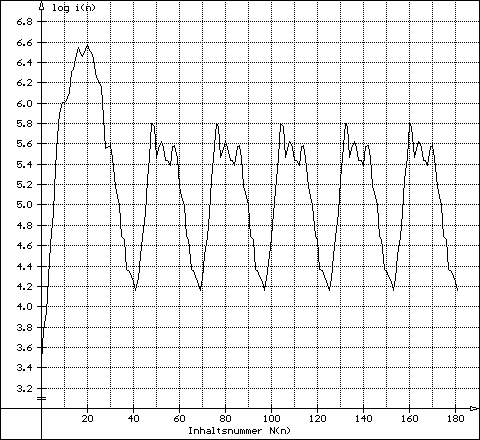
up 840 976950 980460 17490 2856 276 1578 down
276 - open-end sequence
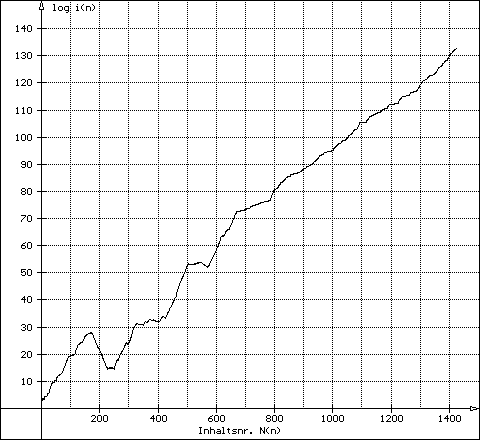
up 840 976950 980460 17490 2856 276 1578 down
1578 - OE-sequence with deep minimum
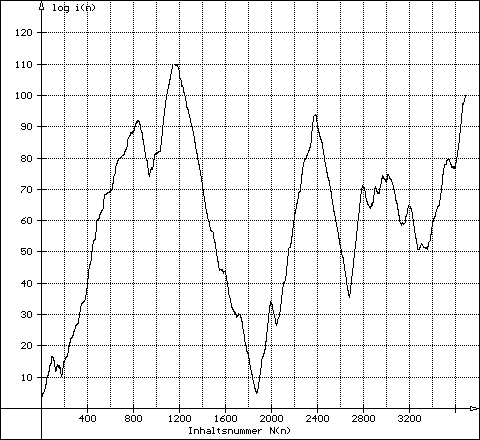
(for greater picture click here or above)
up 840 976950 980460 17490 2856 276 1578 down
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
1) The data of the aliquot sequences in [1, 1000000] includes the data base
C9C30.
Here you'll find all information about terminating and
open-end sequences. There you will find the first 9digit-number (C9) and the
first 30digit-number (C30) of all sequences. With this data it will be possible
to identify side-sequences.
2) A second data base C60
shows the first 60digit-number of every sequence. It will be possible to
identify some more side-sequences.
3) In spring 2000 calculations up to C80 began. A third database is in
progress. The main part was finished in march 2003. You will find the first part here: C80
C9C30 - part / C60 - part / C80 - part
C9C30 / C60 / C80 - complete (zipped for download)
4) Aliquot needs a matrix (record
file). Each number corresponds to a target. There are different possibilities
for an entry:
a) -1 if n has not yet been looked at
b) a prime if the sequence starting with n ends in this prime
c) a positive nonprime integer (the smallest member of an aliquot cycle) if the
sequence ends in a perfect number, in an amicable pair or cycle
d) a negative number, if the sequence is an OE-sequence (the entry is the
negative key-number)
With this categories you can sort all entries easily.
There are only entries of such sequences which were computed
with UBASIC-programs in the
base-matrix. It's easy to change entries in such a matrix. Its easy to
calculate a base-matrix, too. To change a totally calculated record file is more
difficult because not all side-sequences can be changed.
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
The following internet pages give more information about this subject:
aliquot sequences - Primzahlfamilien
amicable numbers - aliquot cycles
Mersenne primes - perfect numbers
For German users the following websites are useful: A guide to the complex website of Chris Caldwell is the mask of Tobias Jentschke (in German) with effectively set links. The subject has been reviewed in a newspaper article in Mario Jeckle's website. Both websites link directly to a page with a biography of Marin Mersenne. Udo Hebisch shows an actual table of Mersenne primes. Caldwell renders short biographies of living mathematicians on a further page.
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
You will not find many books in German. There are only a few
older mathematical articles. The following link will show you a bibliography
of printed documents.
David Moews,
Eric W. Weisstein
and Chris K. Caldwell
give an actual overview about the English literature. In German
the following book summarizes most of all:
Wolfgang Creyaufmüller: "Primzahlfamilien - Das
Catalan'sche Problem und die Familien der Primzahlen im Bereich
von 1 bis 3000 im Detail", 19951, 176 p. / 19972, 262
p. / 20003, 327 p.
ISBN 3-9801032-2-6.
Here you will find a great bibliography and commented programs
for PCs with complete source code. The following bibliography-link shows the
actual
mathematical part of the 3rd edition.
An interesting website you will find by Scott Contini's FactorWorld. There are download-possibilities for many papers.
Computing aliquot sequences creates problems in factorizing at an early stage. You seldom
see this inside a terminating sequence with a low maximum. If the sum of
divisors like in OE-sequences normally increases you will often find only smaller primes
fast (example 276).
There remains a greater rest - a composite integer - seldom with more than two prime factors. To factorize this
composite number is hard and time-consuming.
Normally you will not find any rule how to compute them, but you can crack the
factors with the programs below.
ECM
- Factorizing with elliptic curves
During the last few years a lot of factorizations have been carried out very
effectively with ECM-method, a computing technique using elliptic curves.
Programs on this base
will find factors up to 20 digits fast. That means in minutes or in a few
hours. Factors up to 30 digits you will normally find in a few hours, seldom in
days. For greater factors you need luck!
A new record is the 54digit prime found by ECM at 26. Dec. 1999. You will find
the most interesting information on the
ECMNET
page of Paul Zimmermann.
PPMPQS
- Factorizing with multiple polynomial quadratic sieves
To factorize a really great integer you can use a multiple polynomial quadratic sieve (PPMPQS),
too. For a 100digit-number you need a few weeks computation time. In autumn 2001
was the record at 109 digits. Use the links
below for downloading the latest UBASIC
versions of PPMPQS.
Number Field Sieve (Nfs)
Up to now I couldn't test the complete number field sieve myself. I couldn't integrate
the number field sieve into the program for calculating aliquot sequences, too.
But you will find literature and programs on the website of
Conrad Curry (this link is dead from time to time) or on the website of Henrik
Olsen.
The best website in this days is Paul
Leyland's. There you will find an excellent description
of the whole theme.
Some papers you will find at nfs-Papers.
Good information you will find in mathworld,
too.
An interesting site for a gnfs-implementation: GGNFS.
There is one method to run GGNFS in a DOS-Window under
WinXP actually. NFS is god for C98 composites as minimum. The speed is pretty
good, NFS runs about 20 times faster than ECM or PPMPQS. These values are approximately.
A) First you have to install ActiveRearl: Free
Active Pearl
B) You need some binaries. You will find them under this link: Free
GGNFS
C) You must install NFS with its folders.
D) All this you will find in this ZIP-file: ggnfs.zip
Start the number sieve in the subdirectory "TESTS" and execute num
with the number you want to factorize.
There are sieves for special and sieves for arbitrary numbers (general nfs). In
teamwork we cracked a C111-cofactor in the sequence 276 with Nfs,
but each of us did only a part of the work with a part of the program. The
record in May 2007 is a C307-factorization
(C200-factorisation in May 2005), (C174-factorisation
in December 2003),
( C158-factorisation in February 2003)
by Jens Franke.
It exist
a new implemented Ubasic version
of Nfs from Yuji Kida. It runs
only with the experimental version Ubasic 9.
Factorizing great integers is a part of cryptography and together with this a
question of data security.
You will find a description of all common factorizing methods on the website of Jim Howell.
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
The programs I used are written in Turbo Pascal and in
UBASIC.
UBASIC is
especially for mathematical use and for computation with great
numbers. It's normally freeware. You can factorize integers up to a limit of 105 digits with the DOS version of
Yuji Kida's PPMPQS,
a multiple polynomial sieve. The
actual Windows version computes up to 120 digits . Both methods are integrated in my programs
for aliquot sequences. All programmes will run in Windows 7 in a DOS-Box
with less comfort.
Other Programs
Comment:
ALIQUOT is written by Ivo
Duentsch
in Turbo Pascal and available in its original version at the ftp-server. The
expanded German versions
AQCN and
AQSN
for statistics are the base of the table above. Both programs were patched in
February 2001. The old version created the well known "Borland-Turbo-Pascal-runtime-error
200".
The UBASIC-programs Ellixts.ub,
Ellippmp.ub and Ellppmpx.ub
are totally given in
the source code. They are freeware, too.
You can use them and test your own variations, for example at school ...
Ellippmp.ub and Ellppmpx.ub
alternate automatically between calculation with Ecm
and calculation with Ppmpqs.
Both converters
Alq2elf
und Elf2alq are written by Jesper
Gerved. They are useful for condensing the data-files (*.ELF).
In December 2001 Clifford Stern wrote a helpful program to find out the
confluence-point of side-sequences. A second program converts SQ-files into
*.ELF-files.
You will find other programs for other hardware in the
web. Have a look on Richard Pinch's page for computer algebra. On my page are
mainly information about DOS/Windows-computer and programs for this machines. Paul
Zimmermann
gives a lot of information about UNIX-computers and programs for calculations.
On this page you will find many useful links, too. Some examples below:
Hisanori Mishima has a new factorization
program from Satosi Tomabechi: Ppsiqs.
It is said to be faster than Ppmpqs.
| ECM - PPMPQS - PPSIQS | NFS | General |
| ECMNET - free available ECM programs | Number Field Sieve | Algorithmische Zahlentheorie |
| ECM client/server | Number Field Sieve Org. | Jim Howell |
| Hisanori Mishima | GGNFS | Richard Pinch's Computer Algebra Links |
| Arithmétique Théorie des Nombres | Wikipedia-GNFS | MIRACL - Michael Scott |
| ECC Tutorial | MSIEVE | Richard Brent's factor tables |
| Elliptic Curves | Wilfried Keller - Faktortafeln | |
| Crypto-World | ||
| Factorization Announcements | ||
| numbertheory.org/ntw/N4.html - links | ||
| Primzahlen - prime numbers | ||
| Prime Links ++ | ||
| Primzahlseite |
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
At school you can use this material in classes 9 up to 12 in mathematics for manual arithmetics. We've applied it several times with great success at Freie Waldorfschule Aachen. computer Sciences we teach in class 11 and 12. Pupils can make their own programs easily. The Project stopped in September 2008 due to energy prices.
December 1999:
The programs for aliquot sequences (DOS version) have been running for several years without any trouble.
The conversion to Windows
(3.x, 9x) has been successful, too.
May/June 2000:
The Ubasic programs Ellixts.ub,
Ellippmp.ub and Ellppmpx.ub
have been modified for factorizations into three primes.
The calculations in (1134, 10000] (Varona) have been interrupted at indices
between C91 and C100.
The calculations of 921232 (record aliquot sequence) have been interrupted at index 5326.
October 2000:
The programs
Ellippmp.ub and Ellppmpx.ub
got a bug fix.
December 2000:
All sequences in [900000, 10^6] are calculated up to a new limit:
Generally C80. There are now 987 OE-sequences in this interval.
May 2001:
All sequences in [800000, 900000] are calculated up to a new limit:
Generally C80. There are now 982 OE-sequences in this interval.
October 2001:
All sequences in [100000, 200000] are calculated up to a new limit:
Generally C80. There are now 975 OE-sequences in this interval.
January 2002:
All sequences in [200000, 300000] are calculated up to a new limit:
Generally C80. There are now 938 OE-sequences in this interval.
March 2002:
All sequences in [300000, 400000] are calculated up to a new limit:
Generally C80. There are now 877 OE-sequences in this interval.
May 2002:
All sequences in [400000, 500000] are calculated up to a new limit:
Generally C80. There are now 917 OE-sequences in this interval.
July 2002:
All sequences in [500000, 600000] are calculated up to a new limit:
Generally C80. There are now 971 OE-sequences in this interval.
January 2003:
All sequences in [600000, 700000] are calculated up to a new limit:
Generally C80. There are now 958 OE-sequences in this interval.
March 2003:
All sequences in [700000, 800000] are calculated up to a new limit:
Generally C80. There are now 961 OE-sequences in this interval.
This was the last step - in [1, 10^6] all OE-sequences are calculated up
C80 or higher. About 17% of all numbers in [1, 10^6] - exactly 171251 - are
members of these 9486 OE-sequences.
July 2003:
The calculations in [50000, 100000] are finished. All sequences reached
a maximum of 10^90 (Creyaufmueller/Stern).
August 2004:
The calculations in (10000, 50000] (Bosma) are still running, too.
All sequences reached a maximum of 10^90, about 50% more than 10^90.
The calculations ran completely new up to 10^100 (Creyaufmueller). This work is done.
The calculations in (1000, 10000] (Varona/Benito) are still running. All
sequences reached a maximum of 10^100. The calculations have been stopped.
September 2005:
The calculation in (50000, 100000] will be extended up to C100. This work
is finished.
June 2008:
All sequences in [100000, 200000] are calculated up to a new limit:
Generally C100. There are now 961 OE-sequences in this interval.
September 2008:
1) At the moment computations in the sequences 276,
564, 660
and 966
are running (Zimmermann/Howell/Creyaufmueller).
2) The statistics of aliquot sequences in [1, 1000000] will be
actualized from time to time. The complete results includes the data base
C9C30.
Here you'll find all information about terminating and
open-end sequences. There you will find the first 9digit-number (C9) and the
first 30digit-number (C30) of all sequences.
3) A second data base C60
shows the first 60digit-number of every sequence in [1, 10^6].
4) A third data base C80 shows the first
80digit-number of every sequence in [1, 10^6]. There are combined results from Zimmermann,
Varona, Creyaufmueller, Bosma.
5) The calculations in (1000, 10000] will be extended by
Christopher Clavier.
6)
The calculation in (200000, 250000] will be extended up to C100. About 40%
of these computations are finished.
7) The calculation in (250000, 300000]
will be extended up to C100 by Wieb Bosma.
8) The first sequence reached the record index 8033.
June 2009:
All OE-Sequences are
online for download
Since January 2010:
A group of free workers will do lots of work on aliquot sequences. To avoid
multiple work please check the website of Mersenne-Forum
for reserved sequences! (200k, 250k] is up to >C100. (500k, 600k] is reserved,
(700k, 800k] too.
October 2011:
The first OE-sequence reached more than index 10000 with actually i12320 (C150)
January 2016:
The first sequence reached C200 ( 2340, 28-01-2016, Tom Womack).
| C9C30 - last update: 12-8-2009 | C60 - last update: 17-5-2002 | C80 - last update: 31-3-2003 |
| Data base C9C30 - partition 1 to 100000 |
Data
base C60 - partition 1 to 100000 |
Data
base C80 - partition |
| Data base C9C30 - complete version (ca: 650 kB) |
Data
base C60 - complete version (ca. 372 kB) |
Data
base C80 - complete version (ca. 446 kB) |
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
Please compare this table with Clifford Sterns page and his graphs
|
sequence |
status |
graph |
date |
first computed or maximum reached by |
|
| Record length: | i4015: OE-sequence | g204838 | Creyaufmueller/ Zimmermann |
||
| ( i > 4000 ) | 635016 | i4090: side-sequence to 25968 | Creyaufmueller | ||
| 227646 | i4203: side-sequence to 25968 | Creyaufmueller | |||
| 652500 | i4208: side-sequence to 25968 | Creyaufmueller | |||
| 43974 | i4126/i4243: OE-sequence | 13-06-2004 | Bosma / Creyaufmueller | ||
| 481900 | i4346: terminates in 3 | 31-08-2009 | mataje | ||
| 43230 | i4356: terminates to 101 | g43230 | 03-12-1999 | Bosma | |
| 604440 | i4368: OE-sequence | 03-01-2003 | Creyaufmueller | ||
| 98790 | i4443: terminates to 13 | 20-07-2008 | Stern/Creyaufmüller | ||
| 971088 | i4468: OE-sequence | 05-10-2000 | Creyaufmueller | ||
| 216840 | i4699: OE-sequence | 24-08-2008 | Creyaufmueller | ||
| 446580 | i4736: terminates to 601 | g446580 | 19-04-2002 | Creyaufmueller | |
| 321090 | i4743: OE-sequence | 29-01-2002 | Creyaufmueller | ||
| 11040 | i4746/i4853: OE-sequence | 22-12-2001 09-06-2004 |
Stern Creyaufmueller |
||
| ( i > 5000 ) | 643752 | i5008: OE-sequence (C83) | 06-12-2002 | Creyaufmueller | |
| 92898 | i5063: terminates to 41 | 11-03-2010 | Stern | ||
| 696780 | i5293: terminates to 59 | 09-02-2010 | frmky | ||
| 921232 | i5326: OE-sequence (C103) | g921232 | 03-06-2000 | Creyaufmueller | |
| 59232 | i5339: OE-sequence (C102) | 21-01-2001 | Zimmermann/Stern | ||
| 115302 | i5415: OE-sequence (C100) | g115302 | 24-07-2001 | Creyaufmueller | |
| 8760 | i5583: OE-sequence (C107) | 27-01-2003 | Varona | ||
| 707016 | i5932: terminates in 41 | 12-11-2010 | Batalov | ||
| (i > 6000) | 921232 | i6358: terminates to 11 | g921232-n |
12-04-2010 |
Creyaufmüller/unconnected |
| 483570 | i6491: OES-sequence | 23-05-2002 | Creyaufmueller | ||
| (i > 7000) | 144984 | i6531: OE-sequence / i7053 | 31-08-2007 | Creyaufmueller/Schickel | |
| 1578 | i7147: OE-sequence (C128 ?) / i7261 | 22-11-2006 | Clavier | ||
| 195528 | i7955: OE-sequence | 2009 | Batalov | ||
| (i > 8000) | 389508 | i7070: OES-sequence (C87) / i7135 (C101) / i8000 (C124) / i8033 /C126) | g389508 | 20-03-2002/ 06-12-2006/ 21-06-2008 |
Creyaufmueller/Bosma Stern/Nelson-Melby |
| (i > 9000) ?? | 314718 | OES-sequence:
314718:i6444 = 4788:i6 // i9004 (??) |
2009 (?) 14-07-2010 |
Bosma / Schickel | |
| 11040 | i9405: OE-sequence | 29-03-2012 | unconnected | ||
| (i > 12000) | 933436 | OE-sequence:
933436: i12320 (C150) OE-sequence: 933436: i12516 (C183) |
19-10-2011 29-05-2016 |
unconnected | |
| Terminating sequences: | 64962 | i2595 = 7 | Zimmermann | ||
| 6160 | i3026 = 601 | g6160 | 25-12-2001 | Varona | |
| 42660 | i3057 = 43 | Bosma | |||
| 849920 | i3336 = 7 | 27-03-1999 | Creyaufmueller | ||
| 11670 | i3534 = 193 | 05-09-2007 | Stern | ||
| 483616 | i3616 = 31 | 14-05-2002 | Creyaufmueller | ||
| 62850 | i3973 = 41 | 04-09-2008 | Stern | ||
| 481900 | i4346 = 3 | 31-08-2009 | mataje | ||
| 43230 | i4356 = 101 | g43230 | 0 3-12-1999 | Bosma | |
| 98790 | i4443 = 13 | 20-08-2008 | Stern | ||
| 428106 | i4717 = 7 | 20-01-2012 | Batalov | ||
| 446580 | i4736 = 601 | g446580 | 19-04-2002 | Creyaufmueller | |
| 92898 | i5063 = 41 | 11-03-2010 | Stern | ||
| 696780 | i5293 = 59 | 09-02-2010 | frmky | ||
| 707016 | i5932 = 41 | 12-11-2010 | Batalov | ||
| 921232 | i6358 = 11 | g921232-n |
12-04-2010 |
Creyaufmüller/unconnected | |
| 414288 | i6584 = 601 | 24-07-2009 | Santos | ||
| Side-sequences: | 42800 | i2180 = 4788:i6 = 60564 | Bosma | ||
| 336048 | i2727 = 552: i21 = 772840 | Creyaufmueller | |||
| 389508 | i2919 = 34908:i7 = 113464 | 20-03-2002 | Creyaufmueller | ||
| 487140 | i2960 = 660: i25 = 14700 | 10-10-1998 | Creyaufmueller | ||
| 731520 | i3328 = 4116: i7 = 42028 | 11-02-1999 | Creyaufmueller | ||
| 644664 | i3882 = 37632:i2 = 149716 | 26-12-2011 | bchaffin | ||
| 207984 | i4215 = 53802: i151 = 1773682 | 31-12-1011 | Batalov | ||
| 483570 | i4656 = 1920:i81 = 98624 | 17-05-2002 | Creyaufmueller | ||
| 438966 | i4720 = 5738:i5 = 246584 | 11-02-2012 | unconnected | ||
| 314718 | 314718:i6466 = 4788:i6 = 60564 | 2009 | Schickel/Bosma | ||
|
|
|
||||
| Maximum at terminating sequences: | 4170: i289 | (C84:lg 83.52) terminates in 79 | Mai 1997 | Bosma | |
| 44922: i1167 | C85: lg 84.77) terminates in 41 | Nov. 1999 | Bosma | ||
| 43230: i967 | (C91: lg 90.13) terminates in 101 | g43230 | 03-12-1999 | Bosma | |
| 16302: i973 | (C94: lg 93.85) terminates in 683 | 31-12-2003 | Creyaufmueller | ||
| 49218: i973 | (C94: lg 93.98) terminates in 59 | 07-07-2004 | Creyaufmueller | ||
| 105384: i2014 | (C96: lg 95.15) terminates in 1210/1184 | 02-04-2004 | Stern | ||
| 6160: i1631 | (C96: lg 95.57) terminates in 601 | g6160 | 25-12-2001 | Varona/Benito | |
| 62832: i1740 | (C100: lg 99.01) terminates in 43 | 28-06-2002 | Stern | ||
| 23910: i1216 | (C100: lg 99.43) terminates in 1210/1184 | 22-04-2004 | Stern | ||
| 3630: i1263 | (C100: lg 99.75) terminates in 59 | g3630 | 10-06-2001 | Varona/Benito | |
| 56368: i2007 | (C102: lg 101.36) terminates in 43 | 06-04-2005 | Stern | ||
| 134856: i746 | (C102: lg 101.42) terminates in 601 |
15-06-2009 |
Batalov | ||
| 21024: i1059 | (C103: lg 102.56) terminates in 1429 | 30-04-2005 | Stern | ||
| 754848: i1049 | (C104: lg 103.49) terminates in 14891 |
31-12-2009 |
Batalov | ||
| 683730: i829 | (C105: lg 104.85) terminates in 59 |
08-05-2011 |
bchaffin | ||
| 721980: i886 | (C106: lg 105.06) terminates in 59 | 15-02-2010 | Greebley | ||
| 767296: i1888 | (C106: lg 105.63) terminates in 31 | 15-05-2011 | unconnected | ||
| 815730: i989 | (C106: lg 105.75) terminates in 1153 | 26-02-2010 | biwema | ||
| 477750: i1199 | (C106: lg 105.76) terminates in 601 | 27-06-2011 | bchaffin | ||
| 557016: i1489 | (C107: lg 106.13) terminates in 43 | 16-03-2011 | Schickel | ||
| 92898: i3390 | (C107: lg 106.29) terminates in 41 | 11-03-2010 | Stern | ||
| 90480: i604 | (C107: lg 106.41) terminates in 59 | 15-07-2010 | smh | ||
| 45984: i841 | (C107: lg 106.50) terminates in 11 | 30-05-2006 | Stern | ||
| 649248: i1568 | (C107: lg 106.79) terminates in 281 |
07-05-2011 |
Stern |
||
| 959916: i602 | (C108: lg 107.17) terminates in 43 |
17-05-2011 |
bchaffin | ||
| 275892: i1257 | (C108: lg 107.22) terminates in 59 | 26-04-2011 | RobertS | ||
| 33672: i2069 | (C108: lg 107.99) terminates in 41 | 05-04-2010 | unconnected | ||
| 930306: i937 | (C109: lg 108.09) terminates in 1153 | 13-05-2011 | Stern | ||
| 15960: i846 | (C109: lg 108.26) terminates in 41 | 03-05-2007 | Stern | ||
| 771108: i597 | (C109: lg 108.37) terminates in 321329 | 06-01-2010 | unconnected | ||
| 877240: i2010 | (C109: lg 108.79) terminates in 41 | 18-06-2011 | bchaffin | ||
| 757512: i748 | (C110: lg 109.04) terminates in 601 | 20-05-2010 | Stern | ||
| 673140: i700 | (C110: lg 109.12) terminates in 41 | 18-07-2011 | bchaffin | ||
| 585600: i598 | (C110: lg 109.45) terminates in 37 | 24-07-2011 | unconnected | ||
| 752976: i556 | (C110: lg 109.49) terminates in 43 | 16-06-2011 | fivemack | ||
| 774360: i786 | (C110: lg 109.76) terminates in 37 | 25-09-2011 | bchaffin | ||
| 829914: i1942 | (C111: lg 110.03) terminates in 37 | 04-04-2010 | biwema | ||
| 734184: i852 | (C111: lg 110.50) terminates in 43 | 25-09-2011 | bchaffin | ||
| 368712: i1413 | (C112: lg 111.13) terminates in 41 | 14-07-2011 | unconnected | ||
| 91008: i1074 | (C112: lg 111.53) terminates in 7 | 05-03-2012 | bchaffin | ||
| 373152: i375 | (C112: lg 111.68) terminates in 601 | 09-02-2011 | RobertS | ||
| 543972: i1135 | (C112: lg 111.69) terminates in 37 | 21-11-2011 | bchaffin | ||
| 98790: i3257 | (C112: lg 111.96) terminates in 13 | 20-07-2008 | Stern | ||
| 734760: i836 | (C113: lg 112.06) terminates in 191 | 02-09-2012 | Winslow | ||
| 142764: i1708 | (C113: lg 112.14) terminates in 11 | 13-11-2011 | bchaffin | ||
| 224560: i1238 | (C113: lg 112.15) terminates in 7 | 09-01-2012 | bchaffin | ||
| 590556: i2314 | (C113: lg 112.25) terminates in 59 | 01-10-2011 | RobertS | ||
| 266224: i683 | (C113: lg 112.61) terminates in 1093 | 22-08-2011 | bchaffin | ||
| 858180: i2818 | (C113: lg 112.75) terminates in 59 | 02-10-2011 | bchaffin | ||
| 940470: i3600 | (C113: lg 112.95) terminates in 59 | 11-03-2012 | unconnected | ||
| 11670: i1067 | (C113: lg 112.96) terminates in 193 | 05-09-2007 | Stern | ||
| 428106: i1880 | (C114: lg 113.44) terminates in 7 | 20-01-2012 | Batalov | ||
| 712068: i1935 | (C114: lg 113.78) terminates in 43 | 12-02-2012 | bchaffin | ||
| 555084: i903 | (C114: lg 113.84) terminates in 59 | 17-07-2012 | Batalov | ||
| 587994: i3177 | (C115: lg 114.07) terminates in 5431 | 18-02-2012 | unconnected | ||
| 133938: i3015 | (C115: lg 114.08) terminates in 601 | 28-03-2012 | unconnected | ||
| 507924: i686 | (C115: lg 114.17) terminates in 43 | 15-09-2009 | Greebley | ||
| 151752: i1175 | (C115: lg 114.67) terminates in 59 | 21-06-2009 | Greebley | ||
| 834216: i1507 | (C115: lg 114.99) terminates in 601 | 15-04-2010 | Batalov | ||
| 701184: i783 | (C116: lg 115.81) terminates in 73 | 28-11-2011 | bchaffin | ||
| 306912: i381 | (C116: lg 115.94) terminates in 41 | 09-07-2011 | Batalov | ||
| 417600: i532 | (C117: lg 116.35) terminates in 43 | 19-02-2012 | Batalov | ||
| 58374: i910 | (C118: lg 117.37) terminates in 601 | 29-12-2012 | fivemack | ||
| 98616: i1041 | (C118: lg 117.41 terminates in 43 | 03-12-2009 | Stern | ||
| 677430: i659 | (C118: lg 117.49 terminates in 59 | 07-09-2012 | Winslow | ||
| 163716: i929 | (C118: lg 117.91) terminates in 37 | 12-06-2009 |
Schickel |
||
| 629718: i1331 | (C119: lg 118.07) terminates in 41 | 16-02-2014 | unconnected | ||
| 327132: i3764 | (C119: lg 118.54) terminates in 41 | 15-02-2013 | fivemack | ||
| 109128: i1435 | (C119: lg 118.75) terminates in 601 | 14-04-2013 | fivemack | ||
| 945360: i839 | (C120: lg 119.08) terminates in37 | 22-11-2014 | unconnected | ||
| 933870: i3165 | (C120: lg 119.17) terminates 181 | 10-12-2012 | Batalov | ||
| 19494: i1547 | (C120: lg 119.92) terminates in 37 | 29-11-2012 | fivemack | ||
| 927468: i1304 | (C120: lg 119.96) terminates in 41 | 05-06-2014 | f1pokerspeed | ||
| 259896: i591 | (C121: lg 120.17) terminates in 1210/1184 | 02-12-2013 | Batalov | ||
| 770580: i2992 | (C121: lg 120.30) terminates in 7 | 05-02-2013 | unconnected | ||
| 843528: i1533 | (C121: lg 120.59) terminates in 1511 | 17-02-2015 | unconnected | ||
| 738288: i1263 | (C121: lg 120.72) terminates in 41 |
17-03-2013 |
unconnected |
||
| 62850: i3227 | (C121: lg 120.98) terminates in 41 | 04-09-2008 | Stern | ||
| 675204: i1760 | (C122: lg 121.85) terminates in 2620/2924 | 30-12-2014 | RobertS | ||
| 860076: i1027 | (C122: lg 121.90) terminates in 7 | 23-04-2015 | unconnected | ||
| 856710: i1264 | (C123: lg 122.19) terminates in 41 | 18-12-2013 | unconnected | ||
| 99240: i763 | (C123: lg 122.27) terminates in 397 | 08-07-2012 | Batalov | ||
| 331202: i1357 | (C123: lg 122.44) terminates in 43 |
20-04-2013 |
firejuggler | ||
| 993438: i1090 | (C123: lg 122.62) terminates in 1741 |
20-05-2013 |
Jatheski | ||
| 228522: i2852 | (C123: lg 122.65) terminates in 109 |
12-05-2014 |
Sergiosi | ||
| 966444: i919 | (C123: lg 122.67) terminates in 1153 |
26-02-2015 |
unconnected | ||
| 707016: i3396 | (C124: lg 123.81) terminates in 41 | 12-11-2010 | Batalov | ||
| 643448: i900 | (C125: lg 124.01) terminates in 601 | 30-12-2014 | Bataloc | ||
| 706200: i1012 | (C125: lg 124.08) terminates in 59 | 31-03-2015 | unconnected | ||
| 660212: i1188 | (C125: lg 124.71) terminates in 73 | 25-09-2014 | Batalov | ||
| 921232: i5510 | (C127: lg 126.67) terminates in 11 | 12-04-2010 | Creyaufmüller/unconnected | ||
| 407856: i955 | (C128: lg 127.71) terminates in 41 | 30-11-2014 | unconnected | ||
| Maximum at OE-sequences: | 1134: i2265 | C134 | 30-01-2004 | Zimmermann/ Creyaufmueller |
|
| 552: i902 | C147 | g552 | 15-05-2005 | Zimmermann | |
| 276: i1567 | C149 | g276 | 11-06-2006 | Zimmermann | |
| 3432: i1098 | C160 | 20-05-2006 | Clavier | ||
|
4788: i2529 4788: i5232 |
C172 C195 |
21-04-2010 20-05-2014 |
Clavier Propper |
||
| 3270: i677 | C188 | 19-02-2013 | Clavier | ||
| 2340: i750 | C200 | 28-01-2016 | Womack | ||
|
|
|||||
| Maximum at OES-sequences: | 72288: i1144 | (C90: lg 89.15) - OES to 11408 | 17-07-2002 | Stern | |
| 532530: i1156 | (C109: lg 108.88) OES to 10532 | 07-07-2011 | bchaffin | ||
| 594228: i969 | (C110: lg 109.46) OES to 38208 | 15-11-2011 | bchaffin | ||
| 644664: i779 | (C112: lg 111.46) OES to 37 | 26-12-2011 | bchaffin | ||
| 207984: i4215 | (C112: lg 111.54) - OES to 53802 | 31-12-2011 | Batalov | ||
| 920468: i1041 | (C114: lg 113.57) - OES to 163716 | 29-03-2012 | Batalov | ||
| 438966: i4720 | (C116: lg 115.63) OES to 5748 | 11-02-2012 | unconnected | ||
| 448476: i862 | (C117: lg 116.29) - OES to 1074 | 01-06-2013 | Batalov | ||
| 273540: i1158 | (C117: lg 116.88) - OES to 3876 | 12-07-2013 | unconnected | ||
| 346848: i1314 | (C119: lg 118.27) - OES to 8844 | 27-05-2013 | Batalov | ||
| 337662: i917 | (C122: lg 121.86) - OES to 30352 | 20-04-2015 | fivemack | ||
| 574344: i1041 | (C124: lg 123.46) OES to 5748 | 17-09-2012 | Stern | ||
| Greatest descent: | 1578 | From C110 down to C5 | 20-02-2005 | Clavier |
Note to aliquot sequences with record length:
The three
side-sequences to 25968
are linked at different points:
227646:i14 = 652500:i2 = 2372658 and 820584:i2 = 635016:i3 and 635016:i962 =
227646:i1094 = 230456;532
25968:i10 = 196188:i409 = 635016:i978 = 652500:i1100 = 227646:i1112.
The sequence 921232
is the first well known aliquot sequence with more than 5000
iterations.
The sequence 389508
is the first well known aliquot sequence with more than 8000 iterations; status:
389508:i8033
The calculations of the sequence 115302
have been stopped at index 5415
(C100).
definition aliquot sequences tables diagrams databases links literature factorizing programs projects records start ©
E-mail: Wolfgang.Creyaufmueller@t-online.de
Back to index
- Back to Index without frames - Activate frames and permanent directory