Das Labyrinth von Chartres
Labyrinth
Eingeschriebene Figuren
Literatur
1. Labyrinth
Labyrinthe sind
keine Irrgärten. Sie haben nur einen einzigen, verschlungenen Weg. Dieser führt
vom Startpunkt zum Ziel auf möglichst großer Strecke.
Labyrinthe
sind seit alter Zeit als Einweihungswege benutzt worden. Dies hat sich bis in
die Gegenwart fortgesetzt. Auch in christlichen Kirchen wurden Labyrinthe
eingebaut. Untersucht man die Geometrie der Bauwerke näher, kann man sogar zu
der Schlussfolgerung kommen, dass manche Kathedrale nach geomantischen
Gesichtspunkten erbaut wurde und die Labyrinthe besondere Orte markieren.
Chartres mit seiner Marien-Kirche (Notres-Dames de Chartres) wird nachfolgend
betrachtet.
|

Bild 1 |
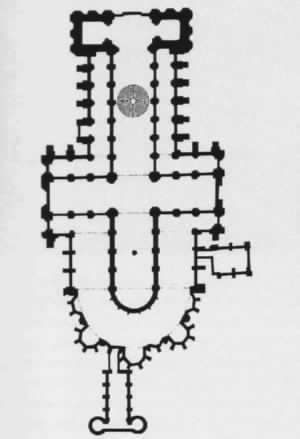
Bild 2 |
|
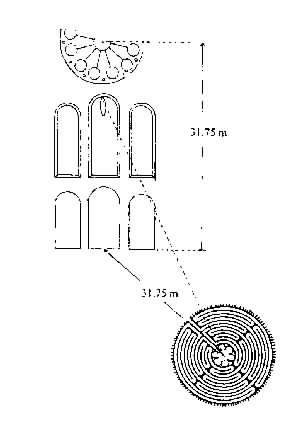
Bild3
|
links oben und unten (Bild 1 und 3):
Die
Korrespondenz von Labyrinth und Westfensterrosette.
links unten (Bild 3):
Die Mandorla im mittleren
Fenster unter der Rosette zeigt den Ort der Maria, deren Bild am 15.
August in die Mitte des Labyrinths projiziert. Die Kathedrale ist der
Maria gewidmet.
rechts oben (Bild 2):
Plan der Kathedrale mit der
Lage des Labyrinths und eines zweiten geomantisch bedeutenden Punktes in
Chor.
aus: Candolini, Gernot, Das geheimnisvolle
Labyrinth, Augsburg 1999, S. 84f. (Bild 2 und 3) und Notre-Dame de
Chartres - l'enigme du labyrinthe, Rectorat de la Cathédrale, o.J., S. 13
(Bild 1).
|
Der Abstand des Labyrinths von der
Eingangswand ist identisch mit der Höhe der Fensterrosette in der Eingangswand.
Dies war sicherlich Absicht der Baumeister und kein Zufall.
Das Labyrinth von Chartres ist somit wohl insgesamt unter dem
Blickwinkel "Nichts ist Zufall" zu betrachten. Interessant wird nun, dass offenbar auch
Zahlengeheimnisse nach pythagoreischem Vorbild eingebaut wurden.

Bild 4: Foto des Labyrinths durch den hohlen Schlussstein des
Gewölbes darüber (in der Kathedrale käufliche Postkarte).
In
diversen Schriften wird die Anzahl der Steinplatten, die den Weg des Labyrinths
bilden, mit 273 angegeben. Dies beruft sich auf die offizielle Darstellung der
örtlichen Bauhütte. Einige Platten sind allerdings gebrochen. Darunter
befinden sich auch solche, bei denen der Bruch sichtlich schon zur Bauzeit
erfolgte und die mit Bruchfuge als zwei Platten gezählt werden müssten. Diese
Zählweise wandte ich an, wenn die Bruchfuge einige Millimeter breit und
sichtbar mit Speis oder Zement verfüllt war. Als einzige Platte zählte ich,
wenn eine Bruchlinie zwar als Haarriss sichtbar, aber nicht verfugt war, denn
ein derartiger Bruch kann auch nach dem ursprünglichen Verlegen der
Bodenplatten erfolgen. Damit erhöht sich die Anzahl der Wegstationen = Platten
auf 276. Wer heute das Labyrinth durchschreitet (was freitags möglich ist),
wird diese Zahl ermitteln können. Damit wird die Frage aktuell, was die
Baumeister mit dieser Zahl verschlüsselt aussagen wollten. Zudem ist jeder, der
nicht auf die wenigen Risse acht gibt, stets im Zweifel über die genaue Zahl.
Wem die Zahl 276 nicht in anderen Zusammenhängen begegnet ist, wird also
vermutlich nichts bemerken.
Was
verbirgt sich also hinter 276 nach pythagoreischem und erweitertem Denkmuster?
Die
folgenden Gedanken befinden sich bestimmt noch in einem keimhaften Stadium,
seien aber trotzdem kurz skizziert. Weil sie sich auf ein mathematisches
Verfahren beziehen, muss dies wenigstens kurz erläutert werden.
Ausführlich ist es in meinem Buch „Primzahlfamilien“ dargestellt:
Pythagoras
wurde einmal gefragt, was denn wahre Freundschaft sei und soll geantwortet
haben, dass wahre Freundschaft zwischen zwei Menschen sich wie die Zahlen 220
und 284 verhalte. Die bleibt unverständlich, wenn man nur auf die Zahlen selbst
blickt. Zerlegt man sie jedoch in ihre Teiler, so findet man bei 220 die echten
Teiler 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 und 110. Zählt man sie zusammen,
ergibt sich als sogenannter Zahleninhalt die Summe 284. Bei 284 mit den Teilern
1, 2, 4, 71 und 142 ergibt sich als Zahleninhalt 220. Seit der Antike werden die
Zahlen 220 und 284 als befreundete Zahlen bezeichnet.
Bildet
man von einer Zahl nach diesem Verfahren den Zahleninhalt und wiederholt dies
mit der erhaltenen und verfährt dann immer so weiter, erhält man eine
sogenannte Zahleninhaltskette. Ein Beispiel hierzu: 20 hat den Inhalt 22, 22 den
Inhalt 14, 14 führt zu 10, 10 zu 8 und 8 zu 7. 7 ist eine Primzahl und hat den
Inhalt 1. Damit endet die Kette. Die meisten Zahlen sind in sogenannte
Primzahlfamilien, also Inhaltsketten mit Seitenzweigen, eingebunden. Sie stecken
grundsätzlich in einer Inhaltskette, die zu einem Ende führt.
In
der Regel ist die Primzahl an Ende klein gegenüber der zu betrachtenden Zahl
und normalerweise sind Inhaltsketten rückläufig, bevor sie in einer Primzahl
enden. Es ist mir bisher nur ein Beispiel einer stets wachsenden Inhaltskette
bekannt, das in einer relativ großen Primzahl (6stellig) endet.
Es
gibt allerdings auch Inhaltsketten, die wachsen, ohne dass ein Ende bekannt ist.
Man nennt sie Offenendketten, kurz OE-Ketten. Die kleinste Zahl, mit der eine
derartige Kette beginnt, ist 276.
Betrachtet
man die Faktoren, die für das Wachstum oder Schwinden einer Kette iterativer
Inhalte verantwortlich sind, die sogenannten Treiber, dann fällt auf, dass 2
bzw. 2er-Potenzen generell Tieftreiber sind, also eine Kette nach unten führen,
eventuell einer Primzahl oder einem sonstigen Ende zu.
Nun
müssen wir einen Blick auf ein wenig mathematisch anmutendes Thema werfen: Bei
der Überschau über die Erdentwicklung im Zusammenhang mit den menschlichen
Inkarnationen machte Rudolf Steiner (GA 102, S.174ff.) darauf aufmerksam,
dass eine Gefahr für die Zukunft einer Entität besteht, wenn sie sich zu tief
mit ihrer jeweiligen Inkarnation verbindet/verwächst. Geschieht dies 16 mal
hintereinander - und eine materialistische Weltsicht bietet hierfür beste
Vorbedingung - fällt ein Mensch aus dem aufwärts strebenden Strom der
Menschheit heraus und muss künftig eine andere Entwickelung unter
Sonderbedingungen antreten. Die Anthroposophie kennt dies unter dem Begriff der
„16 Wege des Verderbens“, weil der Mensch danach aus der Kette der
Inkarnationen ausgegliedert wird.
Eine nach unten gehende, endende Inhaltskette hat auch keine Entfaltungsmöglichkeit
mehr; sie zieht sich auf ein Ziel zusammen und endet - zumindest bleibt im
Bereich der natürlichen Zahlen die Entwicklung der Kette stehen. Denkt man
dies weiter, müssten sich beim Wechsel des Zahlenbereiches auch alle Fragen zur
Teilbarkeit, überhaupt der gesamte Ansatz, einer Metamorphose unterziehen.
Einen anderen Eindruck vom Zahlenwesen erhält man bei Buddha. Der Buddha lehrte
den achtfachen Pfad (auch „achtgliedriger Pfad“ genannt) um den Menschen von
den Folgen seines Karmas zu erlösen. Die Befolgung dieses Erkenntnis- oder
Schulungsweges führt zur Entwickelung des Kehlkopforgans, das auch in der
indischen Literatur als „16blättrige Lotusblume“ bezeichnet wird (Steiner,
GA 114, 8. Vortrag, 24-9-1909).
Der
„Achtfache Pfad (23)“
steht direkt den „sechzehn Wegen des Verderbens (24)“
gegenüber in Wirkung und Absicht; ein Tieftreiber negativer Wirkungen hat
letztlich doch positive Folgen.
Nach
bisheriger Übersicht ist dies erst ein unscharfes Bild, das wohl noch reifen
muss, der Zusammenhang mit der Zahl des Zweifels, der Polarität, gibt aber
dennoch zu denken.
Bei den Inhaltsketten, die sich durch immer größer werdende Zahlen zunehmend
der Berechnung entziehen, sind die Treiber, die kleinen Faktoren, die zu
wachsenden Inhalten führen, häufig vollkommene Zahlen wie 6 und 28. Dies gilt
insbesondere für die Sequenzen, die mit Zahlen unter 1000 beginnen. Es sind
derzeit noch 5 (Lehmer Five). Ihre Startzahlen sind 276, 552, 564, 660, 966. Von
gelegentlichen Schwankungen abgesehen wachsen ihre Inhalte stark an und die
Ketten sind z.Zt. jeweils bis über 110 Dezimalstellen hinaus berechnet. Das
Bild der nach oben strebenden, sich bei zunehmender Differenzierung
erweiternder Sequenzen für die sich entwickelnden, entfaltenden Menschen, im
Zusammenhang mit den vollkommenen Zahlen als Treibern, und das in einer so viel
größeren Menge abnehmender, oder nur teilweise wachsender Ketten respektive
Menschen lässt nachdenklich werden ...
Bisher
fiel mir die erste dieser offenen Ketten mit der Startzahl 276 besonders ins
Auge. An anderer Stelle führte ich
den Zusammenhang zwischen einigen Primzahlfamilien und den 22 Arkana des Tarot näher
aus. 22 Buchstaben, die auch als Zahlzeichen verwendet wurden, hatte das hebräische
Alphabet. Steiner gab zwei relativ kleine Hinweise darauf, dass mit den 22
Bildern die Weltgeheimnisse entschlüsselt werden könnten, wenn es gelänge,
sie richtig in der richtigen Reihenfolge zu lesen. 22 Bilder (oder Gleichnisse ?
) sind die Signatur der vorchristlichen Zeit. Interessant wird nun die nächste
Zahl, die über 22 hinausgeht, also 23 – und hiermit kommt 276 ins Spiel!
Auf
überraschende und für mich ganz neuartige Verbindungen zwischen der ersten
OE-Kette (276) und der Zahl 22 bzw. 23 brachte mich eine schon ältere
Publikation: Ron Jarman (1982, S. 22ff.) enthüllt in seinem kurzen
Artikel einen anderen mathematisch-inhaltlichen Aspekt, der bisher in meinen
Betrachtungen nicht angesprochen wurde. Er verweist auf die so genannten
Dreieckszahlen, deren Eigenschaften schon in der Antike bekannt war und die öfters
benutzt wurden, um geistige Weisheiten zu verschlüsseln. Jarman führt
zwei Beispiele an, die beide im Neuen Testament stehen. Im Johannes-Evangelium
(Kap. 21) wird geschildert, wie die Jünger beim Fischen sind und ihnen der auferstandene
Jesus das dritte mal erschienen ist. Sie ziehen ihren Fang ein und es wird von
153 Fischen im Netz, das nicht zerreißt, gesprochen. 153 ist die Dreieckszahl
von 17, d.h. die Summe der natürlichen Zahlen von 1 bis 17. Von Pythagoras ist
der beispielgebende Ausspruch überliefert: „Was du für 4 hältst ist in
Wirklichkeit (d.h. als Macht) die Zahl 10“
- 1 + 2 + 3 + 4 = 10. Thomas
von Aquin deutete die 153 in 2 Stufen so aus: „153 ist als schöpferisches
Ergebnis der Kraft der 17 ... (wobei) 17 in Wirklichkeit 10 + 7 ist, die
Vereinigung des Irdischen (10 - wir haben 10 Finger, 10 Zehen und haben so ein
dezimales Zählsystem) und des Himmlischen (7 - die Planetenwelten). Die Tat des
Christus war, das Himmlische ganz in das Irdische zu bringen. So ist diese Macht
im Fang der 153 Fische ausgedrückt“ (Jarman, S. 24).
Dieses ausführliche Zitat ist deshalb vorausgeschickt worden, damit das Verständnis
für das zweite Beispiel von Jarman, das sich mit der Zahl 276 beschäftigt,
erleichtert wird. Diese Zahl haben wir weiter oben in anderem Zusammenhang
betrachtet. In der Apostelgeschichte, genauer im 27. Kapitel, wird von der
Seefahrt nach Rom berichtet und deren Unterbrechung durch einen Schiffbruch.
Nach langer, steuerloser Fahrt im Sturm hatte Paulus eine Engelserscheinung mit
der Verheißung, dass alle Menschen auf dem Schiff (bzw. die darauf bleiben)
gerettet werden. Die Zahl derer ist 276. Ron Jarman (S. 25) schreibt
hierzu: „276 ist die Dreieckszahl der Primzahl 23. Was ist Besonderes an 23?
Die alte Kabbala (wörtliche Bedeutung: die Macht der Zwei und Zwanzig) hatte 22
Buchstaben, nämlich 12 (Tierkreis) + 7 (Planeten) + 3 (die Mütter). Aber zu
diesen drei Gruppen brachte der Christus die Vierte - das Ich, das einzig ist.
Also: 23 = 12 + 7 + 3 + 1. Diese neue Macht, die des Christus, ist vereinigt mit
der großen Weisheit der Vergangenheit, sie dabei transformierend. Sie enthüllt
sich im Bild der Rettung aller 276 Seelen.“
Jarman untersucht nun
weiterhin die mathematische Eigenschaft der 23 und stellt fest, dass diese Zahl
die kleinste ist, deren Primzahlring (Z23)
eine Schwelle überschreitet: Ein minimales Erzeugendensystem ist häufig
eine kleine Primzahl. Z23
ist nun der erste Ring,
der nicht von den so genannten Primitivwurzeln 2 oder 3 erzeugt werden kann,
sondern erst von der 5. Dies führt Kowol (S. 80) explizit aus. Jarman
sieht somit die 5 und die 23 in einem engen Zusammenhang und mit der 23 als
Dreieckszahl verbunden die 276 - die erste Schlüsselzahl einer OE-Kette, wie
von mir weiter oben dargelegt wurde.
Kowol (1995, S. 108) führt
zur Zahl 23 noch weitere interessante Aspekte auf; 23 ist die erste Primzahl,
die keinen Primzahlzwilling hat; 23 ist die Anzahl der menschlichen
Chromosomenpaare. Davon sind 22 so genannte Autosome und 1 Paar das
Geschlechtschromosom. Auch hier kann man einen zarten Rückverweis auf den
Zusammenhang des Tarot mit dem Allgemeinmenschlichen erblicken.
Ein
Blick in die Primzahltabelle zeigt, dass 23 die erste Primzahl ist, deren
Zwillingspartner sozusagen einer anderen Gesetzmäßigkeit unterliegt. 25 ist
als Quadrat von 5 eben keine Primzahl. Ab 25 beginnen sich die bis dahin
regelmäßigen vorkommenden Zwillinge aufzulösen. Das unregelmäßige Erscheinungsbild
der Primzahlfolge tritt jenseits von 23 in Erscheinung. 25 ist unter einem
anderen Blickwinkel die „Ersatzzahl“ von 5 zur Familienbildung (vgl. Kap.
11/5). Weiterhin mündet 25 direkt und als einzige Zahl in die kleinste
vollkommene Zahl 6. Diese Gedanken vertiefen den inneren Bezug zwischen 23 und
5 einerseits und über 25 nach 6 sowie in der anderen Richtung zur Dreieckszahl
von 23, zu 276. So kann man über die Zahlen des Menschen - 5 und 22/23 - eine
Verbindung zur ersten vollkommenen Zahl 6 und zur ersten Offenendzahl 276
erblicken.
Lässt
sich die Behauptung wagen, dass mit 276 Wegplatten bis zum Zentrum des
Labyrinths der neue, nachchristliche Weg des Menschen zu seinem waren Kern
verbildlicht wird? Wie bei Pythagoras ist dieser Schlüssel nur dem mathematisch
vorgebildeten zugänglich – ganz im Sinne von L. Locher-Ernst: “Mathematik
als Vorstufe zur Geisterkenntnis“ (so der Buchtitel).
Die Gedanken in diesem Kapitel sind weitgehend originär und stützen sich nicht
auf ältere traditionelle Werke zur Zahlensymbolik. Nach dem oben Angedeuteten
neige ich zur Ansicht, dass die alten Wege nicht weiterführen, neue aber ähnlich
wie bei chaotischen Prozessen üblich, nicht sofort gefunden werden. Erst allmählich
beginnen sich Muster abzuzeichnen. Dies ist mit ein Grund, wieso ein Urteil
tunlichst lange zurückzuhalten ist, bis sich viele Aspekte zu einem neuen Bild
zusammenfügen können. Dass dies möglich ist und vielleicht schon stattfindet,
ist meine tiefe innere Überzeugung.
Deutlich
wurde vielleicht auch, dass die alten Wege der Zahlenbetrachtung für die alten
Schriften ihre Berechtigung hatten, spätestens ab der christlichen Zeit (oder
anders gesagt, dem Neuen Testament) müssen auch hier neue Wege entdeckt und
begangen werden.
Was der Leser mit derartigen Gedankengängen anfangen will, möge ihm selbst überlassen
bleiben. Vielleicht stimmt er aber mit mir darin überein, dass Gedanken, die
Pythagoras anregte und die eingangs unter gegenwärtiger Geistesentwicklung
nach- bzw. weitergedacht wurden, beim Blick auf die Zahlenfamilien neue
Perspektiven eröffnen.
Labyrinth
Eingeschriebene Figuren
Literatur
2.
Eingeschriebene Figuren
Der
Bauplan der Kathedrale insgesamt weist noch viele Maßzusammenhänge auf, die
sicher nicht erschöpfend angesprochen werden können. Die folgenden
Ausführungen resultieren aus Anregungen von Fosar/Bludorf (1996). Die
Autoren machen darauf aufmerksam, dass die Gesamtstruktur der Kathedrale
eine Form verbirgt, die drei mathematische Aspekte verbindet: Irrationalität,
Transzendenz und Goldener Schnitt.
In
den Bauplan des Schiffes mit Chor lassen sich drei Figuren einbeschreiben, die
bestimmt nicht zufällig in diesen Größenangaben gewählt wurden: Ein Kreis,
ein Quadrat und ein Rechteck.
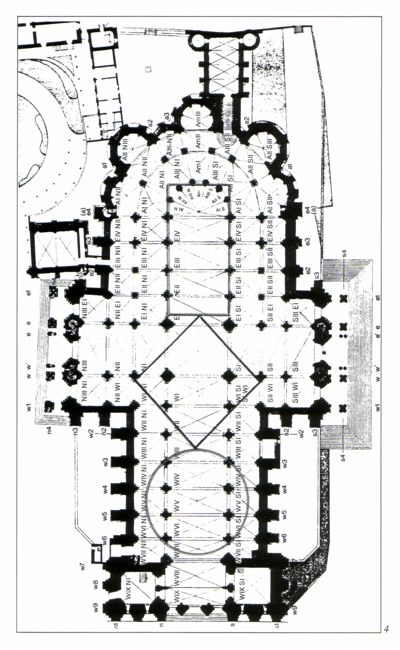
Bild 5: Grundriss der Kathedrale, aus: Fosar/Bludorf, (1996,
Abb. 4)
Geht man vom Rechteck im Chor aus, so hat dies ein
Seitenverhältnis von 1 :2. Nimmt man diese Einheit als Basis, ergibt sich die
Flächenmaßzahl 2. Quadrat und Kreis sind jeweils flächengleich zum Rechteck.
Für das Quadrat bedeutet dies, dass es eine irrationale Seitenlänge hat. Bei
dem Flächeninhalt 2 ergibt sich für die Quadratseite die Wurzel aus zwei.
Für den Kreis bedeutet dies die Aufgabe, ihn flächengleich zum Quadrat
umzuformen - also das antike Problem der Quadratur des Kreises in Umkehrung.
Bekanntlicherweise führt dies auf die Entdeckung der Zahl Pi, die erst gegen
Ende des 19. Jhs. als transzendent erkannt wurde.
Einige Zahlenzusammenhänge, deren tiefere Interpretation
dem Leser überlassen bleiben sollen, weil sie die
hier gewählte Thematik sprengen:
Das Quadrat hat eine Seitenlänge von 23.19m, nach Fosar/Bludorf
(S. 58) ist dies ein Zehntel der Grundseite der Cheopspyramide.
Der Kreis hat somit einem Durchmesser von 26.17m. Er ist etwas mehr als doppelt
so groß wie das Labyrinth, das er vollständig umschließt, allerdings leicht
exzentrisch.
Fosar/Bludorf bringen die drei flächengleichen
Figuren mit den Gralstafeln in Verbindung, die (oder die Kenntnis von ihnen)
direkt den Bau der Kathedrale angeregt haben sollen, nachdem sie von
Tempelrittern aus Jerusalem nach Frankreich gebracht worden waren.
Diese Figuren dienen bei manchen Menschen heute noch als Vexierbilder, die mit
parallel gerichteten Augen betrachtet werden müssen:

Bild 6: "Gralstafeln", aus: Fosar/Bludorf, (1996,
Abb. 5)
Wichtig beim Betrachten ist die Einhaltung
der Abmessungen. Die beiden Reihen sollten etwa auf Augenabstandsweite
auseinander sein.
Zur Hilfe ist ein cm-Maßstab ins Bild eingescannt. Sind die
Augen richtig gerichtet, schieben sich beide Bilder übereinander und es
entstehen erstens Mischfarben und zweitens räumliche Tiefe. Bei geeigneter
Größe des Bildes lässt sich dieser Effekt auch am Bildschirm erreichen.
Ein
dritter Effekt, der sich einstellt, ist ein innerer Zustand der Ruhe und
Harmonie, der durch Synchronisation der Hirnströme erreicht werden soll.
Bei genauer Betrachtung kann man einen kleinen zusätzliche Effekt bemerken: Das
Quadrat erscheint nicht flächig in den Ebene, sondern ist leicht gekippt.
Die obere Spitze kommt dem Betrachter entgegen, die untere beim Kreis
entschwindet nach hinten. Manchmal wird dieses seltsam räumlich Quadrat auch
zum Oktaeder, zur Doppelpyramide (einem der fünf Platonischen Körper). Je nach
Augenstellung kann man vielleicht auch noch mehr entdecken.
Nach den Aussagen von aus: Fosar/Bludorf dienen diese Figuren als
Mittel zur Bewusstseinserweiterung: Die Sehübung ist ein Mittel, das Bewusstsein
zu transzendieren. Weitergehende Aussagen weisen weit über den Bau in Chartres
hinaus und sprengen auch inhaltlich das Thema meiner Erörterung.
Im Originalton lassen sich die Erörterungen
von Fosar/Bludorf auf deren Website nachlesen: Fosar/Bludorf
- Chartres
Labyrinth
Eingeschriebene Figuren
Literatur
Creyaufmüller, Wolfgang
Primzahlfamilien, Stuttgart 2000, 3. Aufl., 327 S.
Creyaufmüller, Wolfgang
TAROT, das Zentrum der Weihnachtsbaumsymbole
Dornach 2000, 47 S.
Fosar, Grazyna / Bludorf, Franz
Das Erbe von
Avalon
München,
1996, 264 S.
Jarman,
Ron
Der Primzahlbereich - Echo dessen, was individuell in der Welt
in: Mathematisch-Physikalische Korrespondenz, Nr. 126, Weihnachten 1982,
Dornach, S. 22-28.
Kowol,
Gerhard
Primzahlen - Ein mathematischer Zugang zu ihren Qualitäten
in: Mathematisch-Astronomische Blätter, Neue Folge, Bd. 18, Dornach
1995, 167 S.
Steiner,
Rudolf
Zur Geschichte und aus den Inhalten der erkenntniskultischen Abteilungen
der
Esoterischen Schule 1904-1914
Gesamtausgabe Nr. 265
Dornach, 1987, 526 S.
4.
Spiel:
Das Labyrinth als Geschicklichkeitsspiel ist
einer Betrachtung wert: http://www.entia.de/Spiel-und-Freude/Fuer-Junge-und-immer-noch-Junge/Das-Labyrinth-von-Chartres.html
(Wolfgang
Creyaufmüller, November 2002 / Oktober 2004 / Juni 2005)
Stand (last update): 22-01-2012
Labyrinth
Eingeschriebene Figuren
Literatur
Zurück zum Index
ohne frames - Aktivierung der frames mit dem permanenten Inhaltsverzeichnis





