This page is available in English, too.
-> Zurück zum Index ohne frames - Aktivierung der frames mit dem permanenten Inhaltsverzeichnis
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
Eine Kette iterativer Zahleninhalte - kurz Inhaltskette (engl.: aliquot sequence) - ist eine Folge von natürlichen Zahlen, die mittels der Teilersummenfunktion gebildet werden: s(n) ist die Summe aller natürlichen Teiler einer Zahl n einschließlich der 1 und n selbst.
Der Zahleninhalt ist die Teilersumme ohne die Zahl n, die sogenannte 'Summe der echten Teiler':
i(n) = s(n) - n.
In der internationalen Literatur
steht für s(n) meist sigma(n). Bei längeren Ketten wird zur
Bezeichnung eines bestimmten Gliedes gewöhnlich die erste Zahl geschrieben
gefolgt von der Indexnummer gleichbedeutend mit "Inhaltsnummer". Ein
Doppelpunkt dient als Trennzeichen.
Beispiel: 276:i4 ist der vierte iterative
Inhalt der Kette, die mit 276 beginnt, also 276:i4 = 1872. Die ersten
Glieder lauten 276, 396, 696, 1104, 1872. Die gesamte
Inhaltskette kann eingesehen werden:
276,
ihr Graph
ebenso (die Beschreibung der graphischen Darstellung erfolgt weiter unten).
Viele Inhaltsketten enden in einer Primzahl. Alle natürlichen
Zahlen, die über Inhaltsketten in ein und derselben Primzahl
enden, bilden eine Primzahlfamilie (andere Abschlüsse sind
möglich; siehe unten). Meistens hat
eine derartige Primzahlfamilie viele Seitenzweige. Neuere Berechnungen führen
gelegentlich zu einem Zusammenfluss (Konfluenz) von bisher getrennten
Inhaltsketten zu einer Familie.
Den übergeordneten Zusammenhang
formulierte erstmals der Lütticher Mathematiker Eugene Charles Catalan im Jahr
1888. Leonard Eugene Dickson erweiterte diese Behauptung zur
heute so genannten Catalan-Dickson-Vermutung, kurz auch immer noch
Catalan'sche Vermutung genannt: "Jede
Kette iterativer Inhalte endet in einer Primzahl oder in einem Ring befreundeter
oder geselliger Zahlen."
Diese Vermutung ist bis heute weder bewiesen noch widerlegt.
Jeder neue Zusammenfluss zweier Inhaltsketten zu einer nährt die Hoffnung auf Erfolge durch Empirie zwar keinen Beweis zu erzielen, aber dennoch an der Lösung des Problems weiter zu arbeiten. Ein beachtlicher Schritt in dieser Richtung geschah im Februar 2005, als Christophe Clavier die Inhaltsketten 1578 und 56440 vereinigte und dabei einen Rekordrückgang entdeckte von 110 auf 5 Dezimalstellen.
Der Begriff "Catalans Vermutung" ist in der Literatur auch für einen anderen Tatbestand gebräuchlich: Catalan behauptete 1844, dass es für die Gleichung xm - yn = 1 nur eine einzige Lösung gibt, nämlich 32 - 23 = 1. Diese Behauptung wurde im Mai 2002 von Preda Mihailescu bewiesen. Dieses Problem wird auf dieser Website nicht untersucht!
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
Endende Inhaltsketten heißen auch terminierte Ketten.
Das normale Ende einer Inhaltskette ist eine
Primzahl.
Anstelle einer Primzahl kann auch ein Ring (Zyklus,
aliquot cycle) das Ende einer Inhaltskette bilden. Bekannt
sind Zweierringe - sogenannte befreundete Zahlen. Pythagoras
verglich wahre Freundschaft mit den Zahlen 220 und 284: i(220) = 284 und i(284)
= 220. Dies ist das kleinste bekannte Paar befreundeter Zahlen. Derzeit sind
nach Pedersen
über 11994387 (am 1-10-2007) befreundete Zahlenpaare bekannt. Nicht alle wurden aufgefunden, die
meisten von ihnen wurden auf der Basis bekannter Zahlenpaare nach sogenannten Thâbit-Regeln
konstruiert. Das
Untersuchungsintervall ist [1, 10^999] mit einigen Erweiterungen in [10^1000,
10^13581]. Bis 10^14 ist die Liste vollständig und die einzelnen Zahlenpaare
mit den Entdeckerangaben können eingesehen werden. Bemerkung: Die Daten bei Pedersen werden in relativ kurzen
Zeitabständen erneuert.
Es sind auch Ringe der Ordnung 4, 5, 6, 8, 9 und 28 entdeckt worden, sogenannte
gesellige Zahlen. Bisher kennt man noch keine anderen Ordnungen, obwohl es für die Zykluslänge meines
Wissens nach keine Begrenzungen gibt. Insgesamt sind derzeit (Februar 2015) 237
Ringe höherer Ordnung bekannt.
Man findet sie bei Moews
aufgelistet. Eine ähnliche Tabelle findet sich auch bei Pedersen.
Die Inhaltskette mit der
Startzahl 17490
mündet in den kleinsten bekannten Viererzyklus. Viererzyklen sind am
häufigsten vertreten: 226 sind bekannt, dazu fünf der Länge 6, drei der
Länge 8 und je einer
der Länge 5, 9 und 28. Vierzyklen sind bis 5*10^12 komplett untersucht. Der
größte Viererzyklus hat 71 Dezimalstellen.
Die kleinsten Ringe sind vollkommene Zahlen. Sie
haben sich selbst zum Inhalt. Die kleinsten dieser Zahlen sind 6,
28, 496, 8128, 33550336. Derzeit sind 48
vollkommene Zahlen
bekannt (die 42. wurde im Februar 2005 gefunden, die 43. Mitte
Dezember 2005, Nr. 44 im September 2006, Nr. 45 im August
2008, Nr. 46 im September 2008, Nr. 47 im Juni 2009, Nr. 48
im Januar 2013). Sie enthalten als Primfaktoren eine Zweierpotenz und
eine Mersenne'sche Primzahl. Bis heute sind nur gerade
vollkommene Zahlen bekannt. Eine ungerade vollkommene Zahl kann nach
Abschätzungen, die 1991 von Brent, Cohen und te Riele gemacht wurden, nicht
kleiner als 10^300 sein.
Im weltweiten
Verbund werden Mersenne'sche Primzahlen gesucht (GIMPS
(engl.) bzw. GIMPS
(dt.)). Die 43. Mersenne'sche Primzahl hat 9152052
Ziffern, die 44. hat 9808358
Ziffern, die derzeit zweitgrößte ist Nr. 45 mit 12978189 Dezimalstellen - die
später gefundenen sind "etwas" kleiner. Die Rekordlänge hat
Nr. 48 mit 17425170 Dezimalstellen.
Vereinzelte Ketten sind offen. Ihre Zahleninhalte wachsen bis zur
derzeitigen Rechengrenze an, ohne dass entschieden werden kann,
ob sie enden oder nicht. Die kleinste Startzahl (auch Schlüsselzahl) einer derartigen Offenendkette
(OE-Kette) ist 276
(-> Labyrinth in
Chartres).
Im Intervall [1, 1000] gibt es 5 offene Ketten. Ihre Startzahlen
sind 276, 552,
564,
660 und
966, die sogenannten
Lehmer Five.
Im Intervall [1, 10000] gibt es zur Zeit 81 Offenendketten, in [1, 100000] gibt es zur Zeit
898 OE-Ketten, in [1, 10^6] gibt es 9190 OE-Ketten. Diese Zahlen sinken mit zunehmendem Rechenfortschritt.
Die folgende Tabelle gibt einen Überblick über den momentanen Rechenstand und
die Bearbeiter (B = Bosma, C = Creyaufmüller, CL = Clavier, G = Gerved, H =
Hoogendoorn, S = Stern, VB = Varona/Benito, Z = Zimmermann);
weitere Details finden sich in einer erweiterten Tafel
[1,
10^6]. Varona listet die Werte
[1,10^4] auf. Die Gesamtübersicht für [1,
220000]
wurde ebenfalls erstellt.
Tabelle -
Gesamtübersicht:
Intervall |
Anzahl der OE-Ketten |
Rechengrenze |
gerechnet von |
| [1, 1000] | 5 | > 10^186 | C/Z |
| [1, 10000] | 81 | > 10^151 | C/VB/Z/CL |
| [1, 50000] | 440 | > 10^100 | B/C/G/VB |
| (50000, 10^5] | 458 |
>10^100 | C/G/S/Z |
| [1, 100000] | 898 | > 10^100 | B/G/Z/VB/S/C/CL |
| (100000, 200000] | 950 | > 10^100 | C/VB |
| (200000, 300000] | 911 | > 10^100 | C / H / B |
| (300000, 400000] | 850 | > 10^80 / 10^100 | C / B |
| (400000, 500000] | 882 | > 10^80 | C |
| (500000, 600000] | 945 | > 10^80 | C |
| (600000, 700000] | 932 | > 10^80 | C |
| (700000, 800000] | 919 | > 10^80 / 10^100 | C |
| (800000, 900000] | 952 | > 10^80 | C |
| (900000, 10^6] | 951 | > 10^80 | C |
| [1,10^6] | 9190 | > 10^80 / 10^100 | |
| Download aller Ketten | > 10^80 / 10^100 | ||
Eine freie Gruppe Mathematiker rechnet im Intervall (500k, 600k]. Um doppelte Arbeit zu vermeiden, bitte die reservierten Sequenzen beim Mersenne-Forum prüfen! (200k, 250k] ist berechnet auf >C100.
Etwa 1% der Zahlen sind Startzahlen für OE-Ketten, d.h. ihre
Primzahlfamilienzugehörigkeit ist unbekannt. Dies ist
eine empirisch ermittelte Größe und kann als Hypothese auch für Bereiche
größer als [1, 10^6] formuliert werden. Allerdings ist anzumerken, dass Richard
K. Guy im sogenannten "Gesetz
der kleinen Zahlen" davor warnte, zu schnelle Schlüsse aus dem
Verhalten kleiner Zahlen zu ziehen - oft gilt nicht für große Zahlen, was für
kleine evident erscheint.
Die komplette Statistik
für [1, 10^6] ist im Anfangsbereich über den vorangehenden link einzusehen,
für einen download klicken Sie hier.
Die obige Tabelle ist das Resultat langjähriger Berechnungen. Mit Hilfe des
Programms
ALIQUOT von
Ivo Düntsch
wurde eine Matrix erzeugt, in der zu jeder natürlichen Zahl das Ziel der auf
ihr aufbauenden Inhaltskette angegeben ist. Für jede Zahl wird also die
Inhaltskette bis zum Ende berechnet oder die Berechnung bricht ab, wenn die
Sequenz zu sehr anwächst. Diese Ketten wurden dann getrennt untersucht. Für
das Intervall [1, 10^6] kam so im Laufe der Jahre ein Datenbestand von mehreren
Gbyte zusammen.
Alle Ketten wurden auf Zusammenhänge untersucht und erfasste
Seitenzweige dem jeweiligen, neuen Ziel zugeordnet bzw. der jeweils kleinsten Startzahl, wenn die Sequenz offen
blieb.
Der gesamte Zahlenbereich bis 10^6 wurde erstmals bis zu einer Obergrenze
von 40 Dezimalstellen durchsucht, später bis zur erweiterten Obergrenze von
mindestens 60 Dezimalstellen (C60). Diese Arbeit war im Mai 1999 vorerst
abgeschlossen.
Seither wurden noch einige Dutzend weitere Ketten terminiert im Zuge der
Erweiterung der Obergrenze auf C80. Die Tabelle
oben enthält den aktuellen Stand. Ende März 2003 waren dann alle OE-Ketten bis
zu einer Obergrenze von mindestens C80 berechnet.
Nach bisherigem empirischem Überblick führt die Erweiterung der Rechengrenze
von C60 auf C80 dazu, dass etwa 2-2.5% der bisher als OE-Ketten eingestuften
Inhaltsketten terminieren oder als Seitenkette identifiziert werden können.
Als an Weihnachten 2001 die Kette 6160 zur Primzahl 601 zuende gerechnet wurde,
wechselten 1797 Zahlen in (1, 10^6], also 1,8%, die Familie.
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
start hoch 840 976950 980460 17490 2856 276 tief
Für einen raschen Überblick ist es günstig, eine
Inhaltskette graphisch darzustellen. Hierzu bietet sich folgende Einteilung der
Achsen an: Auf der x-Achse wird die Inhaltsnummer, beginnend mit 0, aufgetragen
und auf der y-Achse der Logarithmus zur Basis 10 des Inhalts. Wir haben also
eine Funktion f: N(n) -> log10 i(n). Die drei Typen von
Inhaltsketten geben drei Grundtypen in der graphischen Darstellung.
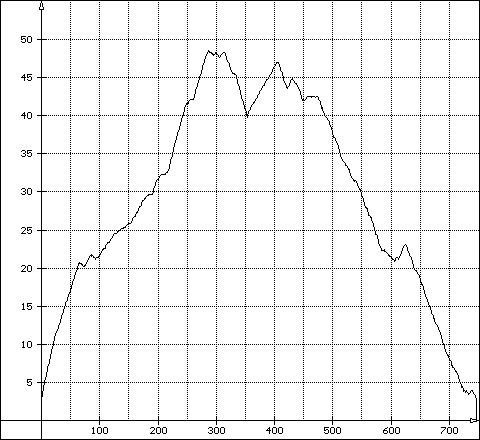
| 1) primterminierte Ketten | Der Graph ist ein einzelner, unregelmäßiger Berg mit einem Hauptmaximum (Ende in Primzahl) | Beispiel: g840 |
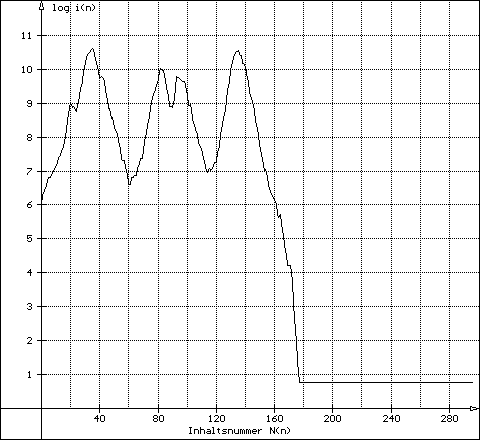
| 2) zyklischer Abschluss | Der Graph endet in einer horizontalen Linie (Ende in vollkommener Zahl) | Beispiel: g976950 |
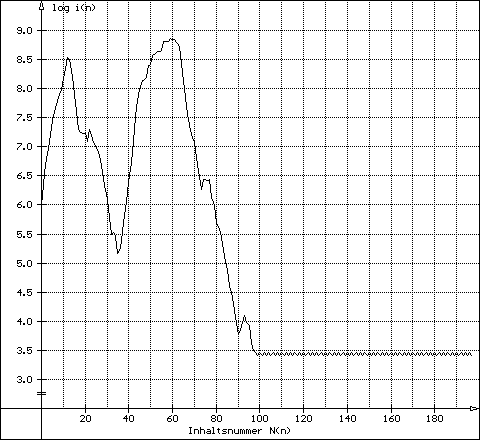
| Der Graph schwankt zwischen zwei horizontalen Grenzgeraden (Ende in befreundeten Zahlen) | Beispiel: g980460 | |
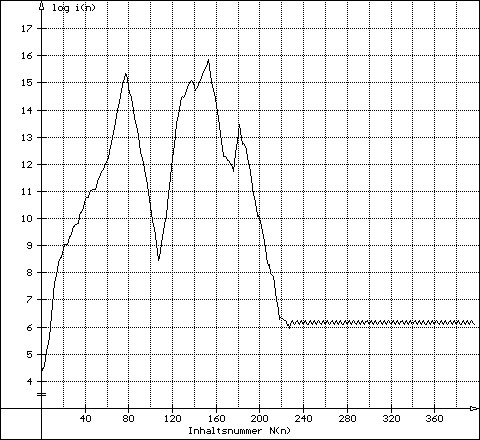
| Der Graph schwankt zwischen zwei horizontalen Grenzgeraden (Ende in einem Zyklus höherer Ordnung) | Beispiel: g17490 und g2856 | |
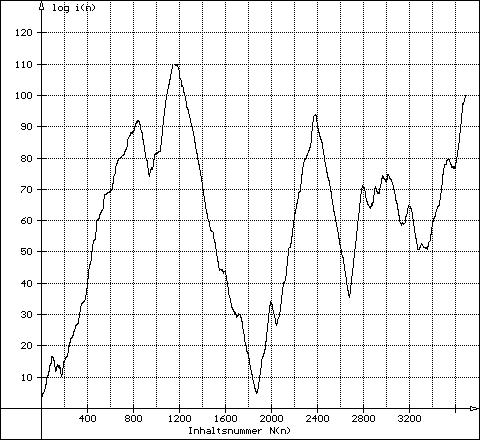
| 3) offene Ketten | Der Graph steigt mehr oder minder konstant an, hat aber sein Maximum zumeist am Ende | Beispiel: g276 und g1578 |
Weitere Graphen sind über die Links in der Rekordliste zu erreichen oder bei den Lehmer Five.
hoch 840 976950 980460 17490 2856 276 1578 tief
840 - primterminierte Kette (Komplette Sequenz)

hoch 840 976950 980460 17490 2856 276 1578 tief
976950 - Abschluss in vollkommener Zahl (6)
hoch 840 976950 980460 17490 2856 276 1578 tief
980460 - Abschluss in einem Zahlenpaar (2620/2924)
hoch 840 976950 980460 17490 2856 276 1578 tief
17490 - Abschluss in 4er-Zyklus
hoch 840 976950 980460 17490 2856 276 1578 tief
2856 - Abschluss in 28er-Zyklus
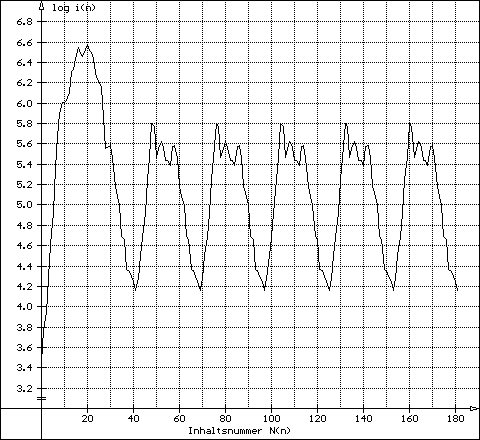
hoch 840 976950 980460 17490 2856 276 1578 tief
276 - OE-Kette
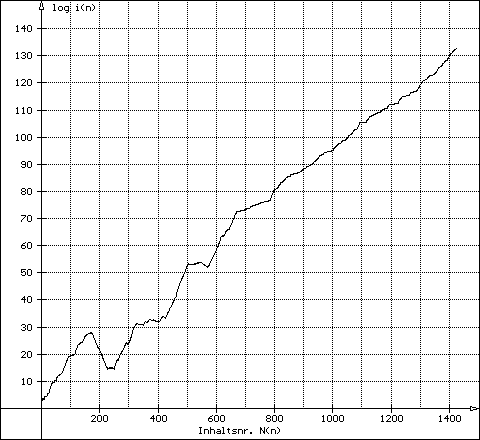
hoch 840 976950 980460 17490 2856 276 1578 tief
1578 - OE-Kette mit Rekordtief
(für mehr Details hier oder oben anklicken)
|
7 |
11 |
13 - 17 - 19 |
23 - 29 - 31 |
|
hoch 840 976950 980460 17490 2856 276 1578 tief
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
1) Die Daten der untersuchten Inhaltsketten im Intervall [1, 1000000] mit ihren
Startzahlen und dem Rechenendstand enthält die
Datenbank C9C30
(über vorstehenden link sehen Sie den Anfangsteil). Hier finden sich terminierte
Ketten und ihre Ziele sowie die OE-Ketten mit den Angaben, wieweit
sie berechnet sind. Zu jeder Kette wird die erste 9stellige Zahl (C9) und die
erste 30stellige Zahl (C30) angezeigt. Mit diesen Werten besteht die
Möglichkeit, Seitenketten zu identifizieren.
2) Eine zweite Datenbank C60
(hier nur der Anfang) zeigt zu jeder Inhaltskette, die auf diese Größe anwächst, ihren ersten
C60-Wert. Diese Zahlen ermöglichten die Identifizierung weiterer
Seitenketten.
3) Im Frühjahr 2000 wurde die erweiterte Berechnung der OE-Ketten bis mindestens
zur Obergrenze C80 begonnen. Ziel ist auch der Aufbau einer C80-Datenbank.
Sie wurde im Dezember 2000 mit den zur Verfügung stehenden Daten aufgestellt
und wurde im März 2003 bis auf allfällige Ergänzungen vollendet.
C9C30 / C60 / C80 - Ausschnitte (zum Betrachten)
C9C30 / C60 / C80 - komplett (gepackt zum download)
4) Zu ALIQUOT gehört eine Matrix (record
file) gleichsam als Gerüst, in der die Einträge zu jeder Inhaltskette zu finden sind. Diese
gliedern sich in verschiedene Gruppen:
a) -1, wenn noch keine Berechnung erfolgte
b) eine Primzahl bei terminierten Ketten
c) die jeweils kleinste, positive Zahl eines Ringes (vollkommene Zahl,
befreundete oder soziale Zahlen)
d) die negativ markierte Startzahl bei OE-Ketten, d.h. wenn ALIQUOT
die Berechnung abgebrochen hat.
Nach diesen Kategorien kann eine Sortierung nach den Gruppen jederzeit erfolgen.
In einer aufgesetzten
Basismatrix finden sich nur die Einträge der Ketten, die mit UBASIC-Programmen
gerechnet wurden. Sie lässt sich leicht anpassen und relativ rasch
durchrechnen. Nachträgliche Änderungen einer fertig gerechneten Matrix sind
allerdings schwierig, weil Seitenzweige oft nicht alle erfasst werden können.
ALIQUOT und zugehörige Matrizen (record files)
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
Unter folgenden Internetadressen finden sich weitere Angaben, teilweise mit vielen Literaturverweisen:
Ein Führer durch die sehr umfangreiche Website von Chris
Caldwell ist die von Tobias Jentschke
aufgesetzte Maske, die mit gut gesetzten links auf die einzelnen Blätter direkt
zugreift. Einen mehr journalistischen Überblick, aber ebenfalls mit vielen
Querverweisen gibt Mario Jeckle.
Beide führen auch direkt zu einer Biographie von Marin Mersenne.
Von Udo Hebisch
stammt eine Website mit der momentan aktuellen Tabelle der Mersenne'schen
Primzahlen und einer Liste mit Lebensdaten bedeutender Mathematiker. Der
Nachteil dieser Seiten ist, dass sie leider seit geraumer Zeit nicht mehr
aktualisiert wurden.
Eine Liste
mit Kurzbiographien
heute aktiver Kollegen gibt Chris Caldwell wieder.
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
Ein aktuelles Verzeichnis
der Schriftdokumente ist über den vorstehenden link zu erreichen.
Überwiegend englischsprachige Literatur findet sich verzeichnet bei
Moews,
Weisstein
und Caldwell und
von da aus über viele links in weiteren Webseiten.
Deutschsprachige Literatur zum Thema ist relativ dünn gesät,
von älteren mathematischen Artikeln abgesehen. Eine aktuelle
Monographie ist:
Wolfgang Creyaufmüller: "Primzahlfamilien - Das
Catalan'sche Problem und die Familien der Primzahlen im Bereich
von 1 bis 3000 im Detail", 19951 ,176 S. / 19972 , 262 S.
/ 20003 , 327 S.
ISBN 3-9801032-2-6.
Hier findet sich die Literatur insgesamt aufgearbeitet.
Programme für PCs sind im Quellcode wiedergegeben. Der Literaturlink führt zum
mathematischen Teil des Inhaltsverzeichnisses der 3. Auflage.
Ein sehr gutes Überblicksverzeichnis mit Download-Möglichkeit der Schriften pflegt Scott Contini mit FactorWorld.
Die Berechnung von Inhaltsketten führt sehr rasch auf
Faktorisierungsprobleme. Bei terminierten Sequenzen mit bescheidenem Maximalwert
fällt dies kaum ins Gewicht. Werden die iterativen Zahleninhalte aber immer
größer - wie es bei OE-Ketten normalerweise der Fall ist; siehe Beispiel
276
- lassen sich häufig nur kleine Primfaktoren leicht abspalten. Es verbleibt
dann ein mehr oder minder großer Rest, der in vielen Fällen zusammengesetzt
ist. Ihn zu zerlegen ist die schwierigste und zeitaufwendigste Tätigkeit. Diese
Restfaktoren gehorchen im Normalfall keiner Gesetzmäßigkeit, sie sind nicht
nach Regeln oder Formel zu erfassen. Ihre Aufspaltung in Primfaktoren ist den
unten angeführten Programmen vorbehalten.
ECM - Faktorisierung mittels elliptischer Kurven
In den letzten Jahren hat sich eine Faktorisierungsmethode mittels sogenannter
elliptischer Kurven bestens bewährt. Programme auf dieser ECM-Basis finden Faktoren
bis zu 20 Dezimalstellen recht schnell, bis zu 30 Stellen innerhalb einiger
Stunden oder Tage. Größere Faktoren werden mit mehr oder minder gutem Geschick
oder Glück aufgespürt.
Mit sehr effektiven Berechnungen wurde am 26. Dezember 1999 der Rekordwert mit
einer 54stelligen Primzahl mittels ECM-Faktorisierung
erreicht. Paul Zimmermann fasst auf seiner Seite zum
ECMNET
Projekt das Wesentliche über die aktuelle ECM-Faktorisierungsmethoden
zusammen.
PPMPQS - Faktorisierung mittels
Siebverfahren
Zuverlässige Zerlegungen großer Zahlen leisten zur Zeit die multiplen
polynomischen quadratischen Siebe (PPMPQS).
Mit ihnen lassen sich hundertstellige zusammengesetzte Zahlen (C100) innerhalb
einiger Wochen faktorisieren. Der Rekord liegt im Herbst 2001 bei 109
Dezimalstellen. Über die links unten können UBASIC
Fassungen für DOS und Windows heruntergeladen werden.
Number Field Sieve - Zahlkörper-Sieb
Das Zahlkörper-Sieb konnte ich noch nicht selbst in
vollem Umfang testen. Mir sind derzeit keine Programme bekannt, die das Zahlkörper-Sieb in
Inhaltskettenberechnungsprogramme einbinden. Es mehren sich aber in den letzten
Jahren die Publikationen
zu diesem Thema. Conrad Curry behandelte
vor einiger Zeit den Komplex auf seiner
Website; er wird zur Zeit weitergeführt von Henrik
Olsen.
Die zur Zeit beste Website wird von Paul
Leyland unterhalten. Hier findet man auch eine grundlegende Einführung
ins Thema.
Literatur zum Thema findet man gesammelt unter nfs-Papers.
Eine ebenfalls gute Zusammenfassung enthält mathworld.
Eine mögliche Verbindung des Zahlkörpersiebes mit den
bisherigen Programmen läuft über MSIEVE
und separate Berechnungen. Die Faktoren müssen in die Inhaltskettenberechnung
derzeit "von Hand" eingefügt werden. Das einzige mir bekannte
Programm, das unter einer WinXP-Umgebung im DOS-Fenster läuft, faktorisiert
Zahlen ab C98 oder größer. Der grob abgeschätzte Geschwindigkeitszuwachs
liegt bei Faktor 20 oder höher. Erste eigene Testrechnungen laufen ab Mai 2008
überaus erfolgreich.
A) Benötigt wird Free
Active Pearl, das als erste Maßnahme zu installieren ist.
B) Als zweites folgen die Binärdateien, die allerdings vom verwendeten
Prozessor abhängen: Free
GGNFS.
C) Der letzte Schritt besteht in der Installation von NFS, das im Verzeichnis
von GGNFS zu platzieren ist.
D) Die gepackte Datei ggnfs.zip enthält alle nötigen Programme. Das
Zahlkörpersieb wird gestartet aus dem Unterverzeichnis "Tests" durch
Eingabe von "num" gefolgt von der zu faktorisierenden Zahl.
Grundsätzlich gibt es zur Zeit Programme für Zahlkörper-Siebe, die spezielle
Zahlen zerlegen (special nfs), aber auch solche für arbiträre Zahlen (general
nfs). Mit einem derartigen
Sieb wurde innerhalb der Sequenz 276 ein C111-Faktor in Teamarbeit zerlegt. Der
momentane Rekord (Mai 2007) ist die Zerlegung einer C307-Zahl
(C200-Zahl im
Mai 2005), (C174
-Zahl
im Dezember 2003), ( C158
-Zahl
im Februar 2003) durch Jens Franke.
Seit kurzem gibt es eine Ubasic-Variante,
implementiert von Yuji Kida. Sie läuft aber nur mit der experimentellen Ubasic-Variante
Version 9.
Ein Hinweis auf eine gnfs-Implementierung: GGNFS.
Die Fragestellung der Faktorisierung großer Zahlen berührt ganz direkt das Gebiet der Kryptographie, d.h. das der Verschlüsselung von Botschaften und ihre Entschlüsselung, letztlich natürlich auch die Sicherheit der gesamten Datenübermittlung.
Einen guten, kompakten, englischsprachigen Überblick über die oben genannten Faktorisierungsmethoden gibt Jim Howell auf seiner Website.
Die momentanen Rekorde, die mittels der verschiedenen Methoden erreicht werden, listet crypto-world auf.
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
Die Programme, mit denen die Berechnungen gemacht werden, sind in
Turbo Pascal und in
UBASIC geschrieben.
UBASIC ist ein Dialekt, der
speziell für mathematische Berechnungen mit großen Zahlen
geeignet ist. Die Programme sind prinzipiell frei erhältlich.
Faktorisierungen von Zahlen bis 105 Dezimalstellen lassen sich
mit der DOS-Version von Yuji Kidas
UBASIC-Progamm
PPMPQS berechnen. Bis 120 Dezimalstellen geht die momentane
Windowsversion. Beide Siebmethoden wurden in das
Inhaltsrechenprogramm eingebunden. Die nfs-Faktorisierungsmethode zerlegt noch
größere Zahlen.
Mit leichten optischen Einschränkungen laufen die Programme auch unter Windows
7 in der DOS-Box.
ALIQUOT und zugehörige Matrizen (record files)
UBASIC-Programme (gepackt zum download) - letzte Änderung: 20-4-2002/29-12-2003/12-6-2004/11-6-2006
ALQ-Konverter (gepackt zum download)
Andere Programme
Kommentar:
ALIQUOT wurde von
Ivo Düntsch
in Turbo Pascal geschrieben und liegt in der Originalfassung auf dem Server in
Belfast.
Das veränderte und erweiterte Programm
AQCN
ist zusammen mit dem ausgegliederten Statistikteil
AQSN
die Basis der ersten Tabelle. Im Februar 2001 wurden beide Programme gepatcht,
weil sie auf Rechnern mit Taktfrequenzen oberhalb 600 MHz den bekannten "Borland
Turbo-Pascal runtime-error 200"
lieferten.
Die UBASIC-Programme Ellixts.ub
und Ellippmp.ub bzw.
Ellppmpx.ub
liegen grundsätzlich im Quellcode
vor und können variiert werden. Sie bieten also alle Möglichkeiten für
unbeschwerten Forscherdrang. Ellippmp.ub
(für DOS pur) bzw. Ellppmpx.ub
(für DOS-Fenster aller Windowsversionen) wechseln automatisch, dies aber einstellbar, zwischen der Berechnung
mittels elliptischer Kurven und der mittels quadratischem Sieb hin und her.
Die beiden Konverter Alq2elf
und Elf2alq sind sehr
hilfreich zum Komprimieren der Zahlendateien (*.ELF) auf weniger als 10% ihres Volumens.
Sie sind von Jesper Gerved geschrieben worden.
Clifford Stern schrieb im Dezember 2001 ein kleines Programm zum
Seitenkettenabgleich und zum Ermitteln des Konfluenzpunktes. Ein zweites
Programm konvertiert SQ-Dateien in ELF-Dateien.
Unabhängig von den Programmen, mit denen die hier
besprochenen Untersuchungen bewerkstelligt wurden, gibt es noch für andere
Hardware entsprechende Software, die prinzipiell dasselbe leisten kann.
Entsprechende Hinweise finden sich z.B. auf Richard Pinch's über
Computeralgebra. Während ich mich maschinenbedingt mit DOS/Windows-Rechnern und
den entsprechenden Programmen beschäftigte, findet man bei Paul
Zimmermann
überwiegend Programme für UNIX-Rechner. Von hier wird man bestens
weitervermittelt, unter anderem auch mit folgenden Links.
Hisanori Mishima gibt auf seiner Seite Hinweise auf ein neues
Faktorisierungsprogramm von Satosi Tomabechi: Ppsiqs
soll schneller sein als Ppmpqs.
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
Ein generelles Ziel ist die didaktische
Umsetzung dieses mathematischen und programmtechnischen Gebiets
für den Oberstufenunterricht in den Klassen 9 bis 12. Das Thema
an sich eignet sich für Unterrichtssequenzen in Mathematik. Es
ist Innerhalb der Oberstufe nahezu altersunabhängig einsetzbar. Grundlegende
Rechentechniken werden in einem neuen Gewand geübt. Die programmmäßige Arbeit dagegen blieb bisher dem
Informatikunterricht der 11. und 12. Klasse vorbehalten. Geübt und erlernt
werden Algorithmen und rhythmologisches Rechnen.
Im laufenden Schulbetrieb an der
Freien
Waldorfschule Aachen werden laufend weitere Erfahrungen gewonnen und vertieft.
Ein Motiv ist die Verbindung der Schüler mit der
Forschungsfront. Aus Energiekostengründen ruht das Projekt seit Herbst 2008.
Dezember 1999:
Die DOS-Versionen der Inhaltsketten-Programme Ellixts.ub
und Ellippmp.ub bzw.
Ellppmpx.ub
laufen seit einigen Jahren
problemlos. Sie wurden in vielen Zwischenschritten verbessert. Die Umstellung von reinen DOS-Programmen auf Windows-Versionen
wurde erfolgreich vollzogen.
Mai/Juni 2000:
Die Ubasic-Siebprogramme Ellippmp.ub
bzw.
Ellppmpx.ub
wurden verbessert für dreifaktorige Zerlegungen.
Juan-Luis Varona beendete die Berechnungen in
(1134, 10000]
Die Berechnung der bislang längsten bekannten Inhaltskette 921232 ist beim Index 5326 vorläufig
gestoppt worden.
Oktober 2000:
Ellippmp.ub
bzw. Ellppmpx.ub
erhielten eine Fehlerberichtigung - bei mehreren kleine Faktoren nach
Neustart stoppte das Programm.
Dezember 2000:
Die Berechnungen in (900000, 10^6] wurden erweitert bis zu einer Obergrenze von
mindestens C80. Es gibt in diesem Intervall jetzt noch 987 OE-Ketten.
Mai 2001:
Die Berechnungen in (800000, 900000] wurden erweitert bis zu einer Obergrenze von
mindestens C80. Es gibt in diesem Intervall jetzt noch 982 OE-Ketten.
Oktober 2001:
Die Berechnungen in (100000, 200000] wurden erweitert bis zu einer Obergrenze von
mindestens C80. Es gibt in diesem Intervall jetzt noch 975 OE-Ketten.
Januar 2002:
Die Berechnungen in (200000, 300000] wurden erweitert bis zu einer Obergrenze von
mindestens C80. Es gibt in diesem Intervall jetzt noch 938 OE-Ketten.
März 2002:
Die Berechnungen in (300000, 400000] wurden erweitert bis zu einer Obergrenze von
mindestens C80. Es gibt in diesem Intervall jetzt noch 877 OE-Ketten. Die Programme Ellippmp.ub
und Ellppmpx.ub wurden erweitert
und verbessert.
Mai 2002:
Die Berechnungen in (400000, 500000] wurden erweitert bis zu einer Obergrenze von
mindestens C80. Es gibt in diesem Intervall jetzt noch 917 OE-Ketten.
Juli 2002:
Die Berechnungen in (500000, 600000] wurden erweitert bis zur Obergrenze von mindestens C80. Es gibt in diesem Intervall jetzt noch 971 OE-Ketten.
Januar 2003:
Die Berechnungen in (600000, 700000] wurden erweitert bis zur Obergrenze von mindestens C80. Es gibt in diesem Intervall jetzt noch
958 OE-Ketten.
März 2003:
Die Berechnungen in (700000, 800000] wurden erweitert bis zur Obergrenze von mindestens C80. Es gibt in diesem Intervall jetzt noch
961 OE-Ketten.
Damit sind alle Berechnungen für 9486 OE-Ketten in [1, 10^6]
abgeschlossen und haben eine Mindesthöhe von 80 Stellen erreicht. Rund
17%, genau 171251 Zahlen aus [1, 10^6] sind Mitglieder dieser OE-Ketten.
Juli 2003:
Die Berechnungen in (50000, 100000] wurden ausgeweitet bis mindestens 10^90 (Creyaufmüller/Stern).
August 2004:
Wieb Bosma rechnete in (10000, 50000] und hat alle Ketten bis
10^90 ausgeweitet, ca. 50% davon bis über 10^90.
Die Berechnungen bis
10^100 sind abgeschlossen. Sie wurden komplett neu erstellt.
Juan Varona und Manuel Benito rechnen in (1000, 10000] - zur
Zeit sind alle Ketten bei 10^100 oder höher. Ihre Berechnungen ruhen derzeit
September 2005:
Die Berechnungen in (50000, 100000] wurden erweitert bis C100. Die
Berechnungen und Kontrollen sind abgeschlossen.
Juni 2008:
Die Berechnungen in (100000, 200000] bis mindestens C100 sind abgeschlossen. Es
gibt in diesem Intervall noch 961 OE-Ketten. Bei der Erweiterung von C80 auf
C100 wurden 15 Ketten terminiert oder als Seitenketten identifiziert.
September 2008:
1) Zur Zeit laufen die Berechnungen der
Inhaltsketten 276,
552, 564,
660
und 966
sowie 1074 und 1134 (Zimmermann/Howell/Creyaufmüller).
2) Die Statistik der Inhaltsketten im Intervall [1, 1000000] wird
ständig aktualisiert. Die gesammelten Ergebnisse enthält die
Datenbank C9C30
(über vorstehenden link sehen Sie den Anfangsteil). Hier finden sich terminierte
Ketten und ihre Ziele sowie die OE-Ketten mit den Angaben, wieweit
sie berechnet sind. Zu jeder Kette wird die erste 9stellige Zahl (C9) und die
erste 30stellige Zahl (C30) angezeigt.
3) Eine zweite Datenbank C60 (hier nur der Anfang) zeigt zu jeder Inhaltskette im Intervall [1, 1000000], die auf diese Größe anwächst, ihren ersten C60-Wert.
4) Eine dritte Datenbank C80 (hier nur der Anfang) zeigt zu jeder Inhaltskette, die auf diese Größe anwächst, ihren ersten C80-Wert. Sie enthält die Ergebnisse von Zimmermann, Varona, Creyaufmüller, Bosma und ist derzeit erstellt für [1, 10^6].
5) Die Berechnungen in (1000, 10000] werden von Christopher Clavier weitergeführt.
6) Die Berechnungen in (200000, 250000] bis mindestens C100 sind zu ca. 40% beendet.
7) Die Berechnungen in (250000, 300000] bis mindestens C100 haben begonnen und werden von Wieb Bosma durchgeführt.
8) Die erste Inhaltskette erreichte die Rekordlänge von über 8000 iterativen Inhalten.
Juni 2009:
Alle OE-Ketten sind zum Download online.
ab Januar 2010:
Eine freie Gruppe Mathematiker rechnet im Intervall (500k, 600k] und in
(700k, 800k]. Um doppelte Arbeit zu vermeiden, bitte die reservierten Sequenzen beim Mersenne-Forum
prüfen! (200k, 250k] ist berechnet auf
>C100.
Oktober 2011:
Die erste Inhaltskette hat im Sommer die Marke von 10000 Gliedern übersprungen
und ist momentan bei Index 12320.
Januar 2016:
Die erste Inhaltskette (28-1-2016, Startzahl 2340) erreicht 200 Dezimalstellen.
| C9C30 Stand: 12-8-2009 | C60 Stand: 27-5-2002 | C80 Stand: 31-3-2003 |
|
Datenbank C9C30 - Ausschnitt 1 bis 100000 |
Datenbank C60 - Ausschnitt 1 bis 100000 |
Datenbank C80 - Ausschnitt |
|
Datenbank C9C30 - Komplettversion (ca. 650 kB) |
Datenbank C60 - Komplettversion (ca. 372 kB) |
Datenbank C80 - Komplettversion (ca. 446 kB) |
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
Bitte auch vergleichen mit Clifford Sterns Seite und seinen Graphen
| Startzahl | Status | Graph | Datum | gefunden bzw. gerechnet von | |
| Rekordlängen: | 204828 | i4015: OE-Kette | g204838 | Creyaufmüller/ Zimmermann |
|
| ( i > 4000 ) | 635016 | i4090: Seitenkette zu 25968 | Creyaufmüller | ||
| 227646 | i4203: Seitenkette zu 25968 | Creyaufmüller | |||
| 652500 | i4208: Seitenkette zu 25968 | Creyaufmüller | |||
| 43974 | i4126/i4243: OE-Kette | 13-06-2004 | Bosma/Creyaufmüller | ||
| 481900 | i4348: terminiert in 3 | 31-08-2009 | mataje | ||
| 43230 | i4356: terminiert in 101 | g43230 | 3-12-1999 | Bosma | |
| 98790 | i4443: terminiert in 13 | 20-07-2008 | Stern/Creyaufmüller | ||
| 971088 | i4468: OE-Kette | 05-10-2000 | Creyaufmüller | ||
| 604440 | i4368: OE-Kette | 03-01-2003 | Creyaufmüller | ||
| 216840 | i4699: OE-Kette | 24-08-2008 | Creyaufmüller | ||
| 446580 | i4736: terminiert in 601 | g446580 | 19-04-2002 | Creyaufmüller | |
| 321090 | i4743: OE-Kette | 29-01-2002 | Creyaufmüller | ||
| 11040 | i4746/i4853: OE-Kette | 22-12-2001 09-06-2004 |
Stern Creyaufmüller |
||
| ( i > 5000 ) | 643752 | i5008: OE-Kette (C83) | 06-12-2002 | Creyaufmüller | |
| 92898 | i5063: terminiert in 41 | 11-03-2010 | Stern | ||
| 696780 | i5293: terminiert in 59 | 09-02-2010 | frmky | ||
| 921232 | i5326: OE-Kette (C103) | g921232 | 03-06-2000 | Creyaufmüller | |
| 59232 | i5339: OE-Kette (C97) | 21-01-2001 | Zimmermann/Stern | ||
| 115302 | i5415: OE-Kette (C100) | g115302 | 24-07-2001 | Creyaufmüller | |
| 8760 | i5583: OE-Kette (C107) | 27-01-2003 | Varona | ||
| 707016 | i5932: terminiert in 41 | 12-11-2010 | Batalov | ||
| (i > 6000) | 921232 | i6358: terminiert in 11 | g921232-n | 12-04-2010 | Creyaufmüller/unconnected |
| 483570 | i6491: OES-Kette (C93) | 23-05-2002 | Creyaufmüller | ||
| (i > 7000) | 144984 | i6531: OE-Kette (C101) / i7053 | 31-08-2007 / 2009 | Creyaufmüller / Schickel | |
| 1578 | i7147: OE-Kette (C128) / i7261 | 22-11-2006 | Clavier | ||
| 195528 | i7955: OE-Kette | 2009 | Batalov | ||
| (i > 8000) | 389508 | i7070: OES-Kette (C87) // i7135 (C101) // i8000 (C124) // i8033 (C126) | g389508 | 20-03-2002 / 60-12-2006/ 21-06-2008 |
Creyaufmüller/Bosma// Stern//Nelson-Melby |
| (i > 9000) ?? | 314718 | OES-Kette: 314718:i6444 = 4788:i6 // i9004 (??) | 2009 (?) 14-7-2010 |
Bosma / Schickel | |
| 11040 | i9405: OE-Kette | 29-03-2012 | unconnected | ||
| (i > 12000) | 933436 | i12320: OE-Kette
(C150) i12516: OE-Kette (C183) |
19-10-2011 29-05-2016 |
unconnected | |
| Längste terminierte Ketten: | 64962 | i2595 = 7 | Zimmermann | ||
| 6160 | i3026 = 601 | g6160 | 25-12-2001 | Varona/Benito | |
| 42660 | i3057 = 43 | Bosma | |||
| 849920 | i3336 = 7 | 27-30-1999 | Creyaufmüller | ||
| 11670 | i3534 = 193 | 05-09-2007 | Stern | ||
| 483616 | i3669 = 31 | 14-05-2002 | Creyaufmüller | ||
| 62850 | i3973 = 41 | 04-09-2008 | Stern | ||
| 481900 | i4346 = 3 | 31-08-2009 | mataje | ||
| 43230 | i4356 = 101 | g43230 | 03-12-1999 | Bosma | |
| 98790 | i4443 = 13 | 20-07-2008 | Stern | ||
| 428106 | i4717 = 7 | 20-01-2012 | Batalov | ||
| 446580 | i4736 = 601 | g446580 | 19-02-2002 | Creyaufmüller | |
| 92898 | i5063 = 41 | 11-03-2010 | Stern | ||
| 696780 | i5293 = 59 | 09-02-2010 | frmky | ||
| 707016 | i5932 = 41 | 12-11-2010 | Batalov | ||
| 921232 | i6358 = 11 | g921232-n | 12-04-2010 | Creyaufmüller/unconnected | |
| 414288 | i6584 = 601 | 24-07-2009 | Santos | ||
| Längste Seitenketten: | 42800 | i2180 = 4788:i6 = 60564 | Bosma | ||
| 336048 | i2727 = 552: i21 = 772840 | Creyaufmüller | |||
| 389508 | i2919 = 34908:i7 = 113464 | 20-03-2002 | Creyaufmüller | ||
| 487140 | i2960 = 660: i25 = 14700 | 10-10-1998 | Creyaufmüller | ||
| 731520 | i3328 = 4116: i7 = 42028 | 11-02-1999 | Creyaufmüller | ||
| 644664 | i3882 = 37632:i2 = 149716 | 27-12-2011 | bchaffin | ||
| 207984 | i4215 = 53802: i151 = 1773682 | 31-12-1011 | Batalov | ||
| 483570 | 483570:i4656 = 1920:i81 = 98624 | 17-05-2002 | Creyaufmüller | ||
| 438966 | i4720 = 5748: i5 = 246584 | 11-02-2012 | unconnected | ||
| 314718 | 314718:i6466 = 4788:i6 = 60564 | 2009 | Schickel/Bosma | ||
| Maximum bei terminierten Ketten: | 4170: i289 | (C84: lg 83.52) endet in 79 | Mai 1997 | Bosma | |
| 44922: i1167 | (C85: lg 84.77) endet in 41 | Nov. 1999 | Bosma | ||
| 43230: i967 | (C91: lg 90.13) endet in 101 | g43230 | 03-12-1999 | Bosma | |
| 16302: i973 | (C94: lg 93.85) endet in 683 | 31-12-2003 | Creyaufmüller | ||
| 49218: i822 | (C94: lg 93.98) endet in 59 | 07-07-2004 | Creyaufmüller | ||
| 105384: i2014 | (C96: lg 95.15) endet in 1210/1184 | 03-04-2004 | Stern | ||
| 6160: i1631 | (C96: lg 95.57) endet in 601 | g6160 | 25-12-2001 | Varona/Benito | |
| 62832: i1740 | (C100:lg 99.01) endet in 43 | 28-06-2002 | Stern | ||
| 23910: i1216 | (C100:lg 99.43) endet in 1210/1184 | 22-04-2004 | Stern | ||
| 3630: i1263 | (C100: lg 99.75) endet in 59 | g3630 | 10-06-2001 | Varona/Benito | |
| 56368: i2007 | (C102: lg 101.36) endet in 43 | 06-04-2005 | Stern | ||
| 134856: i746 | (C102: lg 101.42) endet in 601 | 15-06-2009 | Batalov | ||
| 21024: i1059 | (C103: lg 102.56) endet in 1429 | 30-04-2005 | Stern | ||
| 754848: i1049 | (C104: lg 103.49) endet in 14891 | 31-12-2009 | Batalov | ||
| 683730: i829 | (C105: lg 104.85) endet in 59 | 08-05-2011 | bchaffin | ||
| 721980: i886 | (C106: lg 105.06) endet in 59 | 15-02-2010 | Greebley | ||
| 767296: i1888 | (C106: lg 105.63) endet in 31 | 15-05-2011 | unconnected | ||
| 815770: i989 | (C106: lg 105.75) endet in 1153 | 26-02-2010 | biwema | ||
| 477750: i1199 | (C106: lg 105.76) endet in 601 | 27-06-2011 | bchaffin | ||
| 557016: i1489 | (C107: lg 106.13) endet in 43 | 16-03-2011 | Schickel | ||
| 92898: i3390 | (C107: lg 106.29) endet in 41 | 11-03-2010 | Stern | ||
| 90480: i604 | (C107: lg 106.41) endet in 59 | 15-07-2010 | smh | ||
| 45984: i841 | (C107: lg 106.50) endet in 11 | 30-05-2006 | Stern | ||
| 649248: i1568 | (C107: lg 106.79) endet in 281 | 07-05-2011 | Stern | ||
| 959916: i602 | (C108: lg 107.17) endet in 43 | 17-05-2011 | bchaffin | ||
| 275892:i1257 | (C108: lh 107.22) endet in 59 | 26-04-2011 | RobertS | ||
| 33672: i2069 | (C108: lg 107.99) endet in 41 | 05-04-2010 | unconnected | ||
| 930306: i937 | (C109: lg 108.09) endet in 1153 | 13-05-2011 | Stern | ||
| 15960: i846 | (C109: lg 108.26) endet in 41 | 03-05-2007 | Stern | ||
| 771108: i597 | (C109: lg 108.37) endet in 321329 | 06-01-2010 | unconnected | ||
| 877240: i2010 | (C109: lg 108.79) endet in 41 | 18-06-2011 | bchaffin | ||
| 757512: i748 | (C110: lg 109.04) endet in 601 | 20-05-2010 | Stern | ||
| 673140: i700 | (C110: lg 109.12) endet in 41 | 18-07-2011 | bchaffin | ||
| 585600: i598 | (C110: lg 109.45) endet in 37 | 24-07-2011 | unconnected | ||
| 752976. i556 | (C110: lg 109.49) endet in 43 | 16-06-2011 | fivemack | ||
| 774360: i786 | (C110: lg 109.76) endet in 37 | 25-09-2011 | bchaffin | ||
| 829914: i1942 | (C111: lg 110.03) endet in 37 | 04-04-2010 | biwema | ||
| 734184: i852 | (C111: lg 110.50) endet in 43 | 25-09-2011 | bchaffin | ||
| 368712: i1413 | (C112: lg 111.13) endet in 41 | 14-07-2011 | unconnected | ||
| 91008: i1074 | (C112: lg 111.53) endet in 7 | 05-03-201 | bchaffin | ||
| 373152: i375 | (C112: lg 111.68) endet in 601 | 09-02-2011 | RobertS | ||
| 543972: i1135 | (C112. lg 111.69) endet in 37 | 21-11-2011 | bchaffin | ||
| 98790: i3257 | (C112: lg 111.96) endet in 13 | 20-07-2008 | Stern | ||
| 734760: i836 | (C113: lg 112.06) endet in 191 | 02-09-2012 | Winslow | ||
| 142764: i1708 | (C113: lg 112.14) endet in 11 | 13-11-2011 | bchaffin | ||
| 224560: 1238 | (C113: lg 112.15) endet in 7 | 09-01-2012 | bchaffin | ||
| 590556: i2314 | (C113. lg 112.25) endet in 59 | 01-10-2011 | RobertS | ||
| 266224: i683 | (C113: lg 112.61) endet in 1093 | 22-08-2011 | bchaffin | ||
| 858180: i2818 | (C113: lg 112.75) endet in 59 | 02-10-2011 | bchaffin | ||
| 940470: i3600 | (C113: lg 112.95) endet in 59 | 11-03-2012 | unconnected | ||
| 11670: i1067 | (C113: lg 112.96) endet in 193 | 05-09-2007 | Stern | ||
| 428106: i1880 | (C114: lg 113.44) endet in 7 | 20-01-2012 | Batalov | ||
| 712068: i1935 | (C114: lg 113.78) endet in 43 | 12-02-2012 | bchaffin | ||
| 555084: i903 | (C114: lg 113.84) endet in 59 | 17-07-2012 | Batalov | ||
| 587994: i3177 | (C115: lg 114.07) endet in 5431 | 18-02-2012 | unconnected | ||
| 133938: i3015 | (C115: lg 114.08) endet in 601 | 28-03-2012 | unconnected | ||
| 507924: i686 | (C115: lg 114.17) endet in 43 | 15-09-2009 | Greebley | ||
| 151752: i1175 | (C115: lg 114.67) endet in 59 | 21-06-2009 | Greebley | ||
| 834216: i1507 | (C115: lg 114.99) endet in 601 | 15-04-2010 | Batalov | ||
| 701184: i783 | (C116: lg 115.81) endet in 73 | 28-11-2011 | bchaffin | ||
| 306912: i381 | (C116: lg 115.94) endet in 41 | 09-07-2011 | Batalov | ||
| 417600: i532 | (C117: lg 116.35) endet in 43 | 19-02-2012 | Batalov | ||
| 58374: i910 | (C118: lg 117.37) endet in 601 | 29-12-2012 | fivemack | ||
| 98616: i1041 | (C118: lg 117.41) endet in 43 | 03-12-2009 | Stern | ||
| 677430: i659 | (C118: lg 117.49) endet in 59 | 07-09-2012 | Winslow | ||
| 163716: i929 | (C118: lg 117.91) endet in 37 | 12-06-2009 | Schickel | ||
| 629718: i1331 | (C119: lg 118.07) endet in 41 | 16-02-2014 | unconnected | ||
| 327132: i3764 | (C119: lg 118.54) endet in 41 | 15-02-2013 | fivemack | ||
| 109128: i1435 | (C119: lg 118.75) endet in 601 | 14-04-2013 | fivemack | ||
| 945360: i839 | (C120: lg 119.08) endet in 37 | 22-11-2014 | unconnected | ||
| 933870: i3165 | (C120: lg 119.17) endet in 181 | 10-12-2012 | Batalov | ||
| 927468: i1304 | (C120: lg 119.96) endet in 41 | 05-06-2014 | f1pokerspeed | ||
| 19494: i1547 | (C120: lg 119.92) endet in 37 | 29-11-2012 | fivemack | ||
| 738288: i1263 | (C121: lg 120.72) endet in 41 | 17-03-2013 | unconnected | ||
| 770580: 12992 | (C121: lg 120.30) endet im 7 | 05-02-2013 | unconnected | ||
| 259896: i591 | (C121: lg 120.17) endet in 1210/1184 | 02-12-2013 | Batalov | ||
| 843528: i1533 | (C121: lg 120.59) endet in 1511 | 17-02-2015 | unconnected | ||
| 62850: i3277 | (C121: lg 120.98) endet in 41 | 04-09-2008 | Stern | ||
| 675204: i1760 | (C122: lg 121.85) endet in 2620/2924 | 30-12-2014 | RobertS | ||
| 860076: i1027 | (C122: lg 121.90) endet in 7 | 23-04-2015 | unconnected | ||
| 856710: 11264 | (C123: lg 122.19) endet in 41 | 18-12-2013 | unconnected | ||
| 99240: i763 | (C123: lg 122.27) endet in 397 | 08-07-2012 | Batalov | ||
| 331202: i1357 | (C123: lg 122.44) endet in 43 | 20-04-2013 | firejuggler | ||
| 993438: i1090 | (C123: lg 122.62) endet in 1741 | 20-05-2013 | Jatheski | ||
| 228522: i2852 | (C123: lg 122.65) endet in 109 | 12-04-2014 | Sergiosi | ||
| 966444: i919 | (C123: lg 122.67) endet in 1153 | 26-02-2015 | unconnected | ||
| 707016: i3396 | (C124: lg 123.81) endet in 41 | 12-11-2010 | Batalov | ||
| 653448: i900 | (C125: lg 124.01) endet in 601 | 30-12-2014 | Batalov | ||
| 706200: i1012 | (C125: lg 124.08) endet in 59 | 31-03-2015 | unconnected | ||
| 660212: i1188 | (C125: lg 124.71) endet in 73 | 25-09-2014 | Batalov | ||
| 921232: i5510 | (C127: lg 126.67) endet in 11 | 12-04-2010 | Creyaufmüller/unconnected | ||
| 407856: i955 | (C128: lg 127.71) endet in 41 | 30-11-2014 | unconnected | ||
| Maximum bei OE-Ketten: | 1134: i2265 | C134 | g1134 | 30-01-2004 | Zimmermann/ Creyaufmüller |
| 552: i902 | C147 | g552 | 15-05-2005 | Zimmermann | |
| 276: i1567 | C149 | g276 | 11-06-2006 | Zimmermann | |
| 3432: i1098 | C160 | 20-5-2006 | Clavier | ||
|
4788: i2529 4788: i5232 |
C172 C195 |
21-04-2010 20-05-2014 |
Clavier Propper |
||
|
3270: i677 |
C188 | 19-02-2013 | Clavier | ||
|
2340: i750 |
C200 | 28-01-2016 | Womack | ||
| Maximum bei OES-Ketten: | 72288: i1144 | (C90: lg 89.15) - OES zu 11408 | 17-07-2002 | Stern | |
| 532530: i1156 | (C109: lg 108.88) - OES zu 10528 | 07-07-2011 | bchaffin | ||
| 594228: i969 | (C110: lg 109.46) - OES zu 38208 | 15-11-2011 | bchaffin | ||
| 644664: i779 | (C112: lg 111.46) - OES zu 37632 | 26-12-2011 | bchaffin | ||
| 207984: i2325 | (C112: lg 111.54) - OES zu 53802 | 31-12-2011 | Batalov | ||
| 920478: i1041 | (C114: lg 113.57) - OES zu 163716 | 29-03-2012 | Batalov | ||
| 438966: i3993 | (C116: lg 115.63) - OES zu 5748 | 11-02-2012 | unconnected | ||
| 448476: i862 | (C117: lg 116.29) - OES zu 1074 | 01-06-2013 | Batalov | ||
| 273540: i1158 | (C117: lg 116.88) - OES zu 3876 | 12-07-2013 | unconnected | ||
| 346848: i1314 | (C119: lg 118.27) - OES zu 8844 | 27-05-2013 | Batalov | ||
| 337662: i917 | (C122: lg 121.86) - OES zu 37104 | 20-04-2014 | fivemack | ||
| 574344: i1041 | (C124: .lg 123.46) - OES zu 5748 | 17-09-2012 | Stern | ||
| Größter Rückgang: | 1578 | Von C110 auf C5 | g1578 | 20-02-2005 | Clavier |
Anmerkung zu den Ketten mit Rekordlängen:
Die drei
Seitenketten zu 25968
fließen an unterschiedlichen Stellen ineinander:
227646:i14 = 652500:i2 = 2372658 und 820584:i2 = 635016:i3 sowie 635016:i962 =
227646:i1094 = 230456;
25968:i10 = 196188:i409 = 635016:i978 = 652500:i1100 = 227646:i1112.
Die Sequenz 921232
erreichte als erste bekannte über 5000 Iterationen.
Die Sequenz 389508
erreichte als erste bekannte über 8000 Iterationen; Rechenstand: 389508:i8033
Die Berechnung der
Sequenz 115302 wurde bei
i5415 (C100) vorläufig gestoppt.
Definition Inhaltsketten Tabellen Graphen Datenbanken Links Literatur Faktorisierung Programme Pädagogik Projekte Rekorde Anfang ©
E-Mail des Verfassers: Wolfgang.Creyaufmueller@t-online.de
Zurück zum Index
Zurück zum Index ohne frames - Aktivierung der frames mit dem permanenten Inhaltsverzeichnis